Incrementality testing in Google Ads is suddenly within reach for far more advertisers than before.

Google has lowered the barriers to running these tests, making lift measurement possible even without enterprise-level budgets, as recently reported in Search Engine Land.

That shift naturally raises a question: How is Google able to measure incrementality with so much less data?

For years, reliable lift measurement was assumed to require large budgets, long test windows, and a tolerance for inconclusive results. 

So when Google claims it can now deliver more accurate results with as little as $5,000 in media spend, it understandably sounds like marketing spin.

But it’s not. It’s math.

Behind this change is a fundamentally different testing methodology that prioritizes probability over certainty and learning over rigid proof. 

Understanding how this approach works is essential to interpreting these new incrementality results correctly – and turning them into smarter PPC decisions.

Glossary: Bayesian terms for search marketers

Before we dive in, here are some definitions to refresh your memory from Stats 101. 

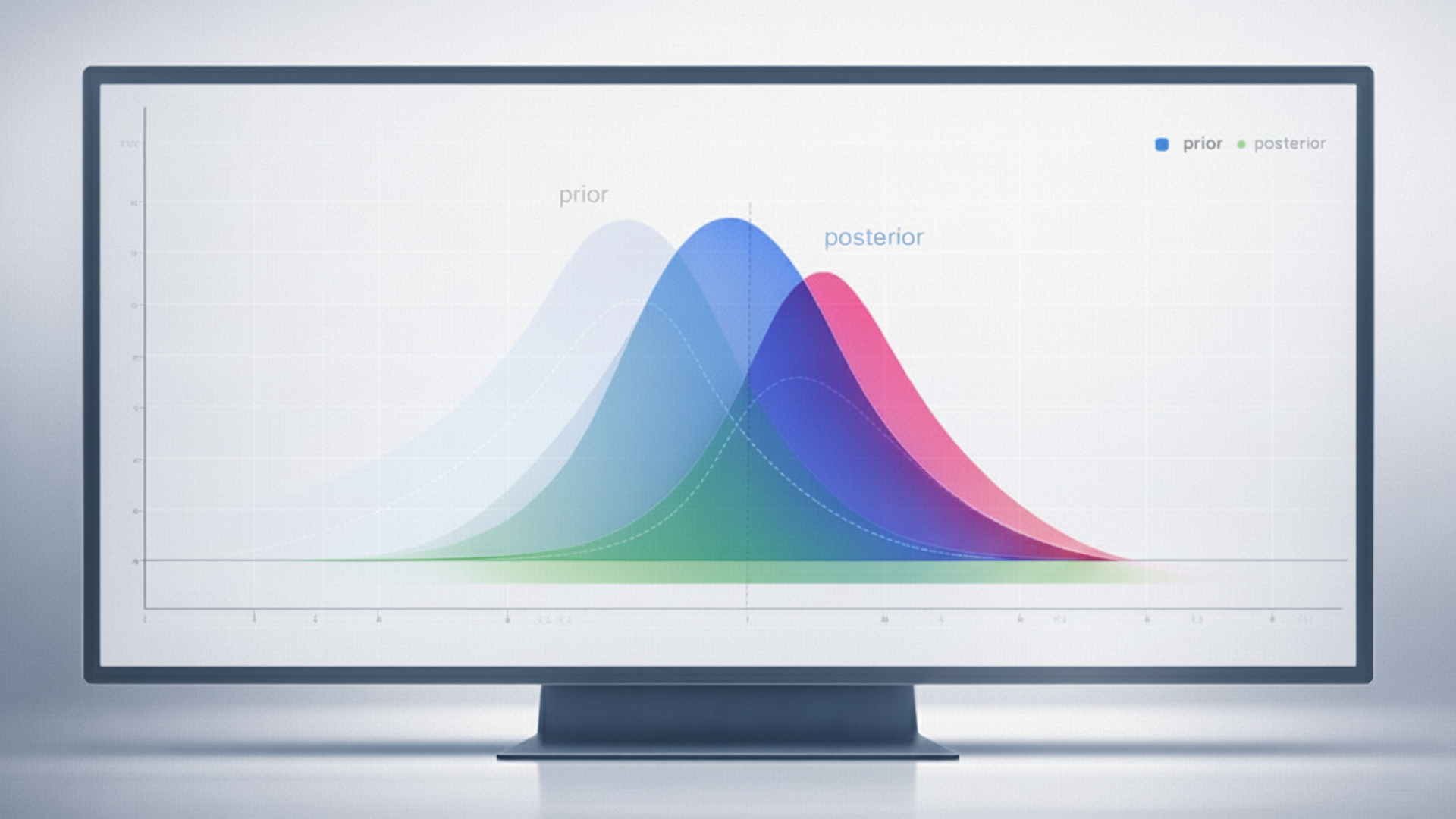
• Prior: What the system believes before the test.
• Posterior: Updated belief after observing data.
• Credible interval: Where the result likely falls (Bayesian).
• P-value: Probability of observing this result if nothing changed (Frequentist).

Why traditional A/B testing fails modern marketers

Most PPC advertisers are already familiar with frequentist statistics, even if they’ve never heard the term.

Any classic A/B test that asks “Did this change reach statistical significance?” and relies on p-values and fixed sample sizes to answer that question is using a frequentist framework. 

It’s the model that underpins most experimentation platforms and has shaped how marketers have been taught to evaluate tests for decades.

Let’s look at what that means for a realistic, smaller-budget test. 

For simplicity, assume a click-based experiment with equal exposure to both variants.

• Total test budget: $5,000.
• Split: 50/50 → $2,500 per variant.
• Average CPC: $2.
• Clicks per variant: 1,250.
• CPA target: ~$100.

Observed results

• Control: 1,250 clicks → 25 conversions → 2.00% conversion rate.
• Treatment: 1,250 clicks → 30 conversions → 2.40% conversion rate.
• Observed lift: 20% more conversions, ~16.7% lower CPA.

On paper, that looks promising: better conversion rate and lower CPA for the treatment.

But when you run a standard two-proportion z-test on those rates, the result tells a very different story.

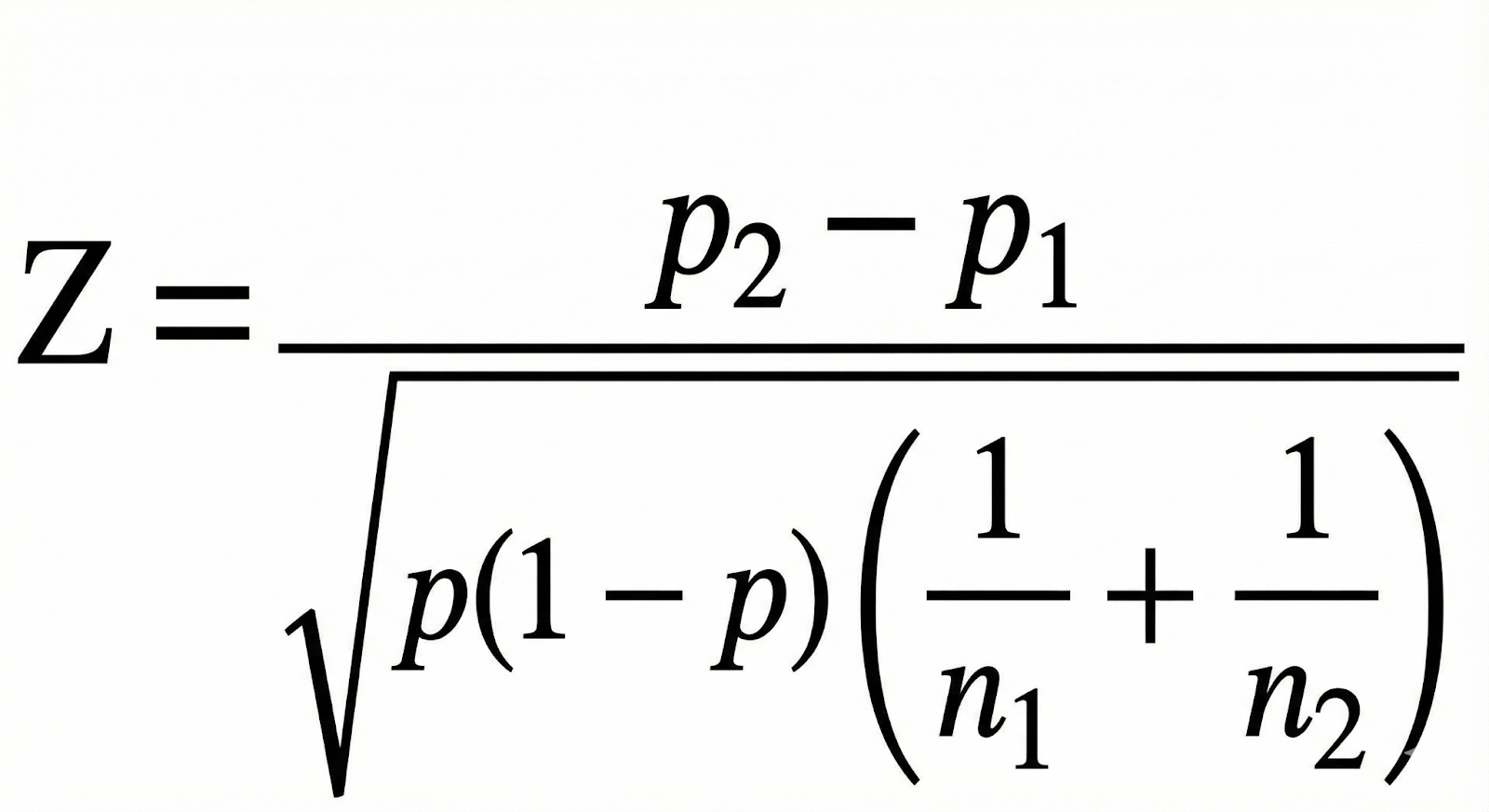
The output looks like this:

• Z ≈ 0.68
• One-tailed p ≈ 0.25
• Two-tailed p ≈ 0.50

In other words, under a traditional frequentist framework, this test is not statistically significant. 

A 20% lift and a visibly better CPA are still treated as “could easily be noise.”

The advertiser has spent $5,000, seen encouraging numbers, but can’t claim a clear winner.

At the budget levels many advertisers can realistically afford, the old-style incrementality tests, which are frequentist in nature, often fail to produce conclusive results.

That’s the gap Google is trying to close with its newer, Bayesian-style incrementality methods: keeping tests useful even when the budget is closer to $5,000 than $100,000.

Here’s why a different approach to the test significantly reduces the required budget.

Dig deeper: Why incrementality is the only metric that proves marketing’s real impact

Bayesian testing: What matters is likelihood, not certainty

Bayesian models ask different – and often more decision-useful – questions. 

Instead of asking whether a result is statistically significant, they ask a more practical question: 

• Given what we already know, how likely is this to be true?

Now let’s apply that framing to the same $5,000 budget example that produced an inconclusive frequentist result.

Using a simple Bayesian model with flat priors (Beta(1,1)):

• Control: 25 conversions out of 1,250 clicks → Beta(26, 1226)
• Treatment: 30 conversions out of 1,250 clicks → Beta(31, 1221)

From these posterior distributions, we can compute:

• Mean lift: ~18–20%
• 95% credible interval: roughly spans negative to positive lift (wide, as expected with small data)
• Probability that lift > 0: ~75–80%

A traditional A/B test looked at the same data and said:

• “Inconclusive. Could be noise. Come back with a bigger budget.”

But a Bayesian read says something more nuanced and infinitely more practical:

• “There’s about an 80% chance the treatment really is better.”

It’s not proof, but it may be enough to guide the next step, like extending the test, replicating it, or making a small allocation shift.

Bayesian methods don’t magically create signal where none exists. So what is the magic then, and why does this work? 

So, how does Google make $5,000 tests work?

Short answer: priors + scale.

Frequentist methods only look at observed test data. 

Bayesian models allow you to bring prior knowledge to the table. 

And guess which company has a ton of data about online ad campaigns? This, indeed, is Google’s advantage. 

Google doesn’t evaluate your test entirely in isolation. Instead, it draws on:

• Informative priors (large volumes of historical campaign data).
• Hierarchical modeling (grouping your test with similar campaigns).
• Probabilistic outputs (replacing p-values with likelihoods).

Google explains these concepts in their Meridian MMM documentation.

Here’s an example:

Test type	Posterior lift	Prob(lift > 0)	Interpretation
No prior	+0.7%	54%	Inconclusive
Prior (~10% lift)	+20.5%	76%	Directionally confident

The prior belief, in the example above, that similar campaigns often see ~10% lift, stabilizes the result enough to support real decisions.

Dig deeper: Exploring Meridian, Google’s new open-source marketing mix model

Smart Bidding already works this way

Should we trust this new approach that uses prior knowledge? 

We should, because it underpins a different system from Google Ads that advertisers are happy with – Smart Bidding. 

Consider how Smart Bidding establishes expectations for a new campaign. It doesn’t start from scratch.

It uses device-level, location-level, time-of-day, vertical, and historical performance data to form an initial expectation and updates those expectations as new data arrives.

Google applies the same principle to incrementality testing.

Your $5,000 test inherits learnings from campaigns similar to yours, and that’s what makes insight possible before spending six figures.

That’s the “memory” behind the math.

Why frequentist thinking leaves marketers stuck

Let’s put Bayesian and frequentist methods side by side:

Aspect	Frequentist	Bayesian
Output	P-value	Probability of lift
Sample size	Large	Smaller if priors are strong
Flexibility	Binary	Probabilistic
Real-world relevance	Limited	High
Handles uncertainty	Poorly	Explicitly

Marketers don’t make decisions in black-and-white terms. 

Bayesian outputs speak the language of uncertainty, risk, and trade-offs, which is how budget decisions are actually made.

---

Google’s data advantage

Google doesn’t guess at priors. They’re informed by:

• Historical campaign performance.
• Cross-campaign learning.
• Attribution modeling (including data-driven attribution and modeled conversions).

Then priors are downweighted as test data accumulates, a core principle of Bayesian statistics and one that’s especially relevant for advertisers concerned about bias or “baked-in” assumptions.

At the start of a test, when data is sparse and noisy, prior information plays an important stabilizing role. 

It provides a reasonable starting point based on how similar campaigns have performed in the past, preventing early results from swinging wildly based on a handful of conversions.

But as more data is observed, something important happens. 

The information coming from the test itself, the likelihood becomes sharper and more informative. 

Each additional conversion adds clarity, narrowing the range of plausible outcomes. 

Over time, that growing body of evidence naturally outweighs the influence of the prior.

In practical terms, this means Bayesian tests don’t stay anchored to their starting assumptions. They evolve. 

Initially, the model relies on historical patterns to interpret limited data. 

Later, it increasingly trusts what actually happened in your campaign. 

Eventually, with enough volume, the results are driven almost entirely by the observed data, much like a traditional experiment.

This dynamic is what makes Google’s approach viable at both ends of the spectrum. 

It allows small tests to produce usable directional insight without overreacting to noise, while still ensuring that large, data-rich tests converge on conclusions driven by real performance rather than inherited assumptions.

What advertisers should watch for

The system is powerful, but not perfectly transparent. Important open questions remain:

• Are priors fully removed once enough test data exists?
• Can advertisers inspect or validate priors?
• What safeguards prevent irrelevant priors from influencing results?

Google has indicated that priors diminish as data grows, but advertisers still need to apply judgment when interpreting results.

Dig deeper: How causal impact studies work and when to use them in PPC

Stop chasing significance, start reducing uncertainty

Statistical significance is a blunt instrument in a world that demands nuance. 

Bayesian testing offers a more practical way to measure impact, especially when budgets are limited and decisions can’t wait.

The next time Google shows you a lift estimate from a $5,000 test, don’t dismiss it.

It’s not smoke and mirrors. 

It’s math with all the benefits of Google’s massive knowledge about the performance of ad campaigns that have come before yours. 

And it’s a welcome new capability from Google Ads for all advertisers who want to make better data-driven optimization decisions.

Apple plans to introduce additional ads within App Store search results starting in 2026, expanding its search ad inventory while keeping strict limits on how advertisers can influence placement.

What’s changing. The new ads will appear inline within App Store search results, alongside organic listings. Existing ads at the top of search results will remain unchanged. Apple says advertisers don’t need to take any action to appear in the new placements — and, notably, they can’t.

What Apple is saying. In guidance shared with Apple Insider, Apple emphasized that relevance is non-negotiable:

• “If your app isn’t relevant to what the user is searching for, it won’t be displayed — regardless of how much you may be willing to pay,” says Apple rep

They continue by saying apps that aren’t a good match for a user’s search query won’t be entered into the auction at all, regardless of bid size. Apple Ads considers both relevance and bids, but relevance is the gatekeeper.

Why we care. Apple is expanding App Store search ad inventory, which could increase competition and change how often ads appear during discovery. At the same time, Apple’s relevance-first approach means bidding alone won’t secure visibility, putting more pressure on keyword strategy and creative quality.

With placement control off the table, advertisers who align closely to user intent stand to benefit most from the added exposure.

What advertisers can control. Creative still matters. Advertisers can prepare multiple ad variations to better align messaging with different audiences or keyword themes. If no custom creative is provided, Apple will automatically generate ads using the app’s product page assets.

Billing stays the same. Apple confirmed there will be no pricing changes. Advertisers will continue to pay per tap or per install, depending on their current setup.

The big picture: Apple has been steadily expanding its ads business. It added ads to the Today tab in 2022 and recently rebranded Apple Search Ads as Apple Ads — signaling broader ambitions, even as it resists traditional auction dynamics seen elsewhere.

The bottom line. Apple is increasing ad density in App Store search, but not advertiser control. More ads are coming — just not the ability to buy your way into better positions.

If you’re leading marketing right now, you’re probably knee-deep in planning season, and feeling a tension I hear from CMOs and VPs every year:

• “We build a plan, but the execution never matches the intent.”

Sound familiar? 

You aren’t alone. 

The disconnect isn’t because goals were wrong or strategies were flawed. It’s because most SEO plans aren’t built to survive operational constraints: 

• Shifting priorities.
• Surprise product launches. 
• Algorithm updates.
• The inevitable “can you just quickly…” requests that derail your roadmap by March.

After helping many businesses build SEO strategies, I’ve learned this: the winners aren’t the ones with the biggest budgets or the flashiest tools. 

They’re the ones with plans built for how work actually gets done, not how we wish it would.

This guide shows you how to create an SEO annual plan that holds up in the real world. 

You’ll learn how to set clear, action-driven goals and build quarterly systems that keep execution on track, even when things get messy.

Why annual planning still works even when everything changes

Annual planning can feel outdated when Google rolls out AI Overviews, ChatGPT and Perplexity emerge as real search alternatives, and algorithm updates land without warning.

Why plan for 12 months when everything could shift next week?

However, businesses that skip long-term planning are often the ones that always play catch-up. 

They’re reactive instead of strategic, chasing trends instead of building assets that compound over time.

An annual plan doesn’t mean you’re locked into every decision for 12 months. 

It means you have clear priorities, allocated resources, and a framework for making smart decisions when things inevitably shift. 

The fragmented search landscape demands better planning

Search is no longer just Google.

Your customers are getting answers from ChatGPT, researching purchases through Perplexity, and discovering solutions in AI-generated summaries that may never send a click to your site.

This fragmentation changes what SEO success looks like. 

It’s not just about ranking, it’s about being the source that AI systems cite and reference. 

It’s about brand authority strong enough that when someone asks an AI assistant about your category, your name comes up.

The fundamentals still matter: quality content, strong technical SEO, and topical authority, but now they serve a broader purpose. 

You’re not just optimizing for Google’s algorithm; you’re building the kind of authoritative presence that gets recognized across platforms.

This is exactly why scattered tactics fail. 

You need a unified strategy that builds brand authority and topical depth, whether someone finds you through traditional search, an AI Overview, or a conversational query to ChatGPT.

A solid annual SEO plan should accomplish three things: 

• Drive real business results (not just traffic).
• Build sustainable competitive advantages through topical authority and quality content.
• Position you to capitalize on changes rather than just react to them.

Setting goals that actually drive execution

Here’s where most SEO plans fail before they even begin: they focus on metrics that don’t directly connect to business outcomes. 

Rankings are nice, but they don’t pay bills. 

Traffic growth feels good, but it’s worthless if visitors don’t convert.

1. Start with performance metrics

What does success actually look like for your business? 

• For ecommerce, that’s revenue from organic traffic. 
• For SaaS, it’s trial signups and paid conversions. 
• For services, it’s qualified leads and booked calls.

Don’t just track these at the top level, segment by landing page and content theme. 

The page driving 1,000 visitors worth $10,000 in revenue beats the one driving 5,000 visitors worth $1,000. Every time. 

This matters when you’re deciding where to invest limited resources.

2. Add visibility metrics with context

Instead of tracking hundreds of individual keyword rankings, focus on keyword groups representing business themes. 

If you sell project management software, track visibility for “project management,” “team collaboration,” and “workflow automation” as distinct groups. 

This gives you a clearer picture of how you’re performing in different market segments.

Share of voice matters more than ever, and not just on Google. 

Monitor whether your brand gets mentioned in AI-generated answers by regularly querying ChatGPT and Perplexity for your key commercial terms and noting whether you’re cited. 

Track your presence across the platforms where your customers actually search. 

If your share of voice is growing across these touchpoints, you’re winning ground. If it’s shrinking, you need to understand why.

3. Build in leading indicators

Annual goals matter, but you need early warning signals. 

If content production slows in Q2, you won’t see the ranking impact until Q4.

If backlink acquisition stalls, authority erodes gradually.

Track metrics like publication frequency, indexation rates, Core Web Vitals scores, and backlink acquisition rate. 

These leading indicators predict future performance in your main KPIs and give you time to course-correct before problems compound.

Dig deeper: SEO execution: Understanding goals, strategy, and planning

The baseline audit: Know where you actually stand

You can’t plan where you’re going without knowing where you are. 

Before building a strategy, you need an honest assessment of your current position. 

Focus on three areas:

Technical health

Can Google find and understand your content? Use Search Console to identify crawl errors, indexation issues, and pages that aren’t getting discovered. 

Check Core Web Vitals on your highest-value pages. These aren’t glamorous, but they’re the foundation everything else builds on.

Content gaps

Map your existing content to the customer journey. Export your top 50 organic landing pages from GA4, then tag each by funnel stage: awareness, consideration, or decision. 

Most businesses discover they’re heavy on awareness content and light on high-intent, bottom-funnel pages. That gap is where your biggest opportunities hide.

Authority signals

Analyze your backlink profile for quality and topical relevance, not just quantity. Search your brand name and see what appears. 

• Are the results positive? 
• Do they accurately represent your business? 

Your online reputation affects both conversions and how search engines perceive your expertise.

This audit consistently reveals surprises, including:

• High-performing pages you may have forgotten about.
• Duplicate content cannibalizing rankings.
• Gaps where you should have content but don’t. 

That clarity is essential for smart prioritization.

---

Building strategy around constraints

Here’s where most planning guidance falls apart.

It tells you what to do, but it ignores the reality of limited resources and competing priorities. 

You can’t do everything, so you need a framework for deciding what to do first.

Use a simple effort-versus-impact matrix to prioritize everything in your plan:

• High impact, low effort
  • Do these first. Fixing obvious technical issues, optimizing existing high-performing content, and targeting low-competition keywords where you can win quickly. 
  • A quick win: find your pages ranking positions 5-15 for valuable terms, often a content refresh and a few internal links can push them onto page one.
• High impact, high effort
  • Schedule throughout the year with adequate resources. 
  • Comprehensive content hubs, major site architecture improvements, and ambitious link earning campaigns. 
  • Don’t stack them all in Q1. Spread the heavy lifting so your team can sustain quality.
• Low impact items
  • Question whether they belong in the plan at all. 
  • Every hour spent on low-impact work is an hour not spent on something that moves the needle.

Your content strategy should begin with understanding customer needs, rather than focusing on keyword volume. 

• What problems are they trying to solve? 
• What information do they need to make good decisions? 

Group related topics into themes that build topical authority, each theme supported by comprehensive pillar content and related cluster pages that demonstrate expertise in that area.

One B2B client I worked with was creating content around every keyword their tools found, but nothing connected. 

We restructured around five core themes tied to their customers’ biggest challenges. 

Within two quarters, their organic traffic to those themes grew 20%, not because they published more, but because they published with intent.

Dig deeper: SEO prioritization: How to focus on what moves the needle

Quarterly execution: Where plans live or die

This is the piece most SEO plans miss entirely, and it’s exactly why execution never matches intent.

Annual plans provide direction, but quarterly execution keeps you moving. 

Break your annual goals into 90-day sprints. 

Each quarter gets 3-5 major deliverables you can realistically achieve with available resources. 

Write them down, assign owners, and set specific completion dates, not “improve technical SEO” but “fix all critical crawl errors and improve LCP on top 20 pages by March 15.” 

It’s better to completely hit fewer goals than partially hit too many.

A typical quarter rhythm might look like this: 

• Q1 focuses on foundational work, including technical fixes, research, and planning major initiatives.
• Q2 and Q3 emphasize execution, including publishing content, building links, and optimizing based on data. 
• Q4 involves measurement, optimization, and planning for next year.

Here’s the critical part most plans miss: reserve 20-30% of your capacity for responding to the unexpected. 

• Algorithm updates happen. 
• Competitors make moves. 
• Market conditions shift. 
• A product launch gets moved up two months. 

You need slack in the system to respond without abandoning your core priorities.

Build review checkpoints into each quarter. 

Block 90 minutes at the end of each month to ask: 

• What’s working? 
• What’s not? 
• What’s changed in the market or search landscape that should influence priorities? 

Keep a running doc of these insights.

Patterns emerge over time that inform smarter planning next year. 

The businesses that adapt quickly during major disruptions typically outperform those who stick rigidly to plans that no longer fit reality.

Monthly check-ins keep projects on track. 

Quarterly reviews allow for bigger strategic adjustments. 

This rhythm creates accountability while preserving the flexibility that separates plans that get executed from those that sit in a folder until next December.

Cross-functional alignment

SEO doesn’t happen in a vacuum. 

• Product teams control roadmaps that impact your site structure. 
• Development teams implement technical improvements. 
• Content and PR teams are natural allies for production and amplification.

Schedule regular sync points with these teams. 

Share keyword research with content creators. 

Work with PR on link earning opportunities. 

Keep stakeholders informed with monthly progress updates that focus on business impact, revenue contribution, and pipeline influence, not just rankings and traffic.

Common mistakes that kill annual plans

Years of building SEO plans reveal a consistent set of failure patterns:

• Too rigid: Plans that can’t adapt to change become irrelevant by March. Build flexibility into the structure, not as an afterthought.
• Too competitor-focused: Understanding competitors matters, but copying their strategy means you’re always a step behind. Focus on serving your customers better than anyone else.
• Too scattered: Trying to do everything means doing nothing well. Most businesses would see better results focusing deeply on fewer areas than spreading thin across every possible initiative.
• Chasing trends over fundamentals: Strong technical foundations, quality content, and good user experience will always matter regardless of algorithm changes. Don’t neglect basics while chasing the latest shiny object.
• Disconnected from business reality: Plans built in isolation from sales cycles, product launches, and seasonal patterns miss opportunities to support broader business goals. Your SEO calendar should align with what’s actually happening in the business.

Dig deeper: SEO strategy in 2026: Where discipline meets results

Making it work

The gap between planning and execution isn’t inevitable.

It happens when plans are built for an ideal world instead of the reality of competing priorities, limited resources, and constant change.

December’s planning session doesn’t have to feel like last year’s. 

Build in the flexibility, focus on the metrics that matter, and create quarterly rhythms that keep execution aligned with intent.

The best plans aren’t the most comprehensive. They’re the ones that actually get executed.

Pages on your website can be well written, well laid out, supported by backlinks, and even meet E-E-A-T expectations – yet still fail to rank.

While there are many possible explanations, one common issue is a misalignment with search intent, and it’s often harder to spot than it sounds.

When the focus is on content, optimization, and usability, intent can easily be missed or misjudged.

This is where AI can become a useful review tool, helping guide things back in the right direction.

Get back to basics

Whether you’re starting work on a new page or updating something older, beginning with the basics of search intent can help set you up for success. 

A simple prompt asking AI for the likely search intents for your given keyword offers a framework to guide your content creation or optimization.

A list of this type will be comprehensive, and you don’t have to hit every variation of intent on the page you create. 

Yet it can highlight different user types, intent shifts, and needs you might not have considered.

Reviewing all these factors will help you create a more useful, well-rounded page that’s likely to satisfy real user needs.

Dig deeper: There are more than 4 types of search intent

Review what’s working

Nailing intent can be harder than it sounds. 

Using AI tools can help you get a feel for what’s already ranking and what those pages are getting right.

AI tools make it easier to get a quick overview of the primary intent of a page. 

You can check this at scale to see whether top-ranking pages all satisfy the same intent. 

Then you can ask the same questions about intent for your page, whether it’s a first draft of something new or an older page you’re optimizing.

If your primary intent matches what’s already succeeding, that’s a great starting point. If it doesn’t, you’ve got a quick answer on how to begin improving it. 

Either way, asking AI tools for suggestions on improvement can give you some useful ideas.

Areas to focus on refining intent can cover the following.

Language

The language you use can reinforce or undermine intent. 

Persuasive, sales-focused wording strengthens commercial intent. 

Descriptive, informative language adds clarity to pages designed to educate or fulfill informational intent.

Format

Even the layout and format of a page give intent signals. 

To offer a couple of examples:

• If it’s a sales page, where do the products sit? 
• What information about them is provided? 
• Does it support sales or product investigation?
• When you’re creating step-by-step guides, have you labeled steps, added visual guides or used video content? 

Calls to action

Giving clear, direct calls to action signifies intent. 

Aligning the action you’d like the user to take with the potential intent underpins the entire purpose of a page. 

Generalized, missing, or uncertain calls to action can dilute both user engagement and ranking.

Dig deeper: How to master user intent with SEO personas

Pricing signals

Have you listed pricing on relevant pages, VAT elements, and currency? 

These can all help send the right signals.

Available support

Is information on or links to pre- or post-sale support readily available? 

Do you have clear contact details for sales teams for user queries? 

Knowing assistance is available could be the difference between making a sale or losing one.

Trust signals

Have you mentioned product guarantees, return policies, reviews, and testimonials? 

All these factors help users make their decision.

Product or service comparison

Clear comparisons between similar products can help with commercial investigation. 

If users are weighing up their options, understanding pros and cons can help move them from research into decision-making.

Dig deeper: How to optimize for search intent: 19 practical tips

---

Improving with structure

As I’ve worked on pages with a specific focus on intent, I’ve discovered areas that try to do too much at once. 

Perhaps this depth of information has worked in the past, but today things need to be clearer, simpler, and more intent-driven.

This has led me to consider where the information really should sit and how it best supports the user journey with new eyes. 

AI tools can help recognize the intent behind specific pockets of information to suggest the best way to structure it. 

Breaking things down into specific guides for different stages of the user funnel can effectively satisfy intent, as well as provide supporting background information for key pages.

An ecommerce example

Let’s consider a sales page for internal French doors. 

The main page is struggling, even though on paper it has plenty of plus points. 

• Detailed copy. 
• Good navigation. 
• A wide product range.

Running the page through an AI tool, along with the top competitors, reveals a pattern.

Competitors are selling first. Your page is problem-solving.

While all the information is useful, it’s not directly addressing the needs of users who have primarily reached the page to purchase or to collect sales-driven information to make a future purchase.

With that in mind, you can adjust the structure:

• Move sales-driven copy to the forefront.
• Address buyer pain points, but keep things concise.
• Move pre- and post-sale information to supporting pages.
• Link all this information together to create a strong hub-and-spoke model.
• Keep the main product listing page sales-focused.

In this scenario, you’re using AI for clarity. It helps you identify the position in the user journey and better satisfy your visitors.

Dig deeper: How to drive SEO growth with structure, skimmability and search intent

Aligning intent for better results

Getting the human aspect of search intent right is the goal, but ranking should follow. 

AI’s biggest strength in this situation is to act like a second set of eyes, helping you interpret patterns and highlight mismatches you might have missed.

Used as a strategic tool, AI can help you:

• Sanity-check your intent alignment.
• Validate what’s working for top competitors.
• Identify structural issues that confuse or dilute intent.
• Strengthen your understanding of your users.

It doesn’t replace expertise, understanding, or skill. 

It helps direct your efforts and fine-tune your approach for better results.

Google Search Console appears to have fixed the month-long delay with the page indexing report just about an hour ago. The report is now showing data as early as a few days ago, which is the normal timeframe for when this report is updated.

Plus, emails about indexing issues have started going out from Search Console to site owners again.

Page indexing report. It shows which pages Google can find and index on your site, along with any problems. You can also submit fixes there and see whether Google confirms they worked. Site owners and SEOs were stuck, they were unable to verify their “fixes” and unable to see if new pages were being indexed and if old pages were having issues being indexed.

Fixed. Here is a screenshot of the report showing December 14th, a much more recent date than the November 21st date that many were stuck on:

Google also fixed the performance reports delay just yesterday. So all the major reports should now be running normally, that is until they break again – which is not that uncommon.

Why we care. Many of you were unable to do full reporting for your SEO clients and stakeholders over the past month. Now you can get recent data both for page indexing and performance reports.

So you should be able to catch up on your reporting before you go into the holiday season.

Googlebot once again generated more traffic than any other crawler in 2025, according to a new Cloudflare report. It outpaced every search and AI bot as Google continued crawling the web for search indexing and AI training.

By the numbers. Googlebot accounted for more than 25% of all Verified Bot traffic observed by Cloudflare.

• Googlebot alone generated 4.5% of all HTML request traffic – more than all other AI bots combined (4.2%).
• AI “user action” crawling surged more than 15x year over year, showing a sharp rise in bots that simulate human behavior.
• Googlebot’s crawl volume dwarfed every other AI crawler, including OpenAI, Anthropic, and Meta.

AI crawling surges. AI crawlers were the most frequently fully disallowed user agents in robots.txt files.

• Anthropic showed the highest crawl-to-refer ratio among major AI and search platforms, meaning it crawled far more content than it sent back as traffic. The ratio peaked near ~500,000:1 early in the year, then settled between ~25,000:1 and ~100,000:1 after May. For comparison:
  • OpenAI spiked to ~3,700:1 in March.
  • Perplexity was the lowest among major AI platforms. It started below 100:1, briefly jumped above 700:1 in late March during a PerplexityBot crawl spike, then stayed mostly below 400:1 and under 200:1 from September onward.

Search platforms looked very different:

• Microsoft hovered between ~50:1 and ~70:1 with a weekly cycle.
• Google rose from just over ~3:1 to ~30:1 by April, fell back to ~3:1 by mid-July, then gradually increased again.
• DuckDuckGo stayed below 1:1 for the first three quarters, then jumped to ~1.5:1 in mid-October and remained elevated.

Google still monopolizes search. Traditional search dominance barely changed.

• Google remained the top search engine by a wide margin, delivering nearly 90% of search engine referral traffic.
• Bing (3.1%), Yandex (2.0%), Baidu (1.4%), and DuckDuckGo (1.2%) rounded out the top five.
• Cloudflare saw minimal movement during the year.
  • Google stayed dominant throughout.
  • Yandex slipped from 2.5% in May to 1.5% in July.
  • Baidu rose from 0.9% in April to 1.6% in June.

The report. The 2025 Cloudflare Radar Year in Review: The rise of AI, post-quantum, and record-breaking DDoS attacks

In this new era of generative AI technology, searchers have begun to swap keywords with prompts. Shorter and long-tail queries are being replaced by more conversational prompts, which tend to be longer and more in-depth. These days, searchers are expecting more complete answers than a paginated list of results.

Until we get an AI-specific equivalent of Google Search Console or Bing Webmaster Tools, we can’t really see for certain what or how our audience is behaving on AI search platforms as they look for our content, brands or products.

However, we can still look for proxies to emulate how this journey works. Here are multiple ways to use other data points as proxies to find prompts used by your audience. You can then use your AI Tracking Tool of choice to track how these prompts are performing.

People Also Ask

Hidden in plain sight, you can use a very popular SERP feature to move from keywords to prompts/questions. People Also Ask (PAA) was introduced in 2014 and suggests multiple related questions to your query. You can easily go from a keyword to a list of questions. When clicking on any PAA result, the list expands and gives you more terms.

Go query by query to find relevant PAAs, or you can use AlsoAsked to extract the exact questions at scale. PAAs are long questions that attempt to answer the next questions asked in the search journey, so they’re a step closer to prompts written in AI Search platforms.

Userbots

Userbots like ChatGPT-User and Perplexity‑User are powerful ways to see how your pages are being used in AI Search. It doesn’t give you the prompts they use, but it’ll help you assess which pages are being cited without trying to guess by tracking prompts that may or may not be relevant at all.

These bots ping the URLs on your website when they’re used to formulate an answer to a user. The process is called RAG (Retrieval-Augmented Generation).

Your customers search everywhere. Make sure your brand shows up.

The SEO toolkit you know, plus the AI visibility data you need.

Start Free Trial

Get started with

To paraphrase Mike King, one of the most trusted sources in SEO & AI, RAG is a mechanism by which a language model can be “grounded” in facts or learn from existing content to produce a more relevant output with a lower likelihood of hallucination.

Translation: Your page was used as an answer and, in some shape or form, your content helped a user. This may give you clues about what type of content is most used by your audience on these platforms, even if the answer hasn’t turned into a click.

Historically, log files have been difficult for SEOs to get, despite every website having them in its servers (yet another reason why SEOs should have access to them!).

You could use a combination of pages with userbot visits, search for their main keywords (as seen on Semrush or GSC), and then see which PAAs Google displayed. 

Long queries on GSC/BWT

Despite not giving a breakdown of AI Mode or AI Overview queries on GSC, smart SEOs are finding proxies that can be used to find queries that resemble the behavior we expect in these platforms. One of them is Ziggy Shtrosberg, who came up with a huge regex you can copy and paste to your GSC.

His guidelines are to:

1. Filter by Search Appearance: Desktop
2. Add a page filter with your root domain (e.g., “https://www[dot]example[dot]com/”) and add this massive regex under the Query filter:

^(generate|create|write|make|build|design|develop|use|produce|help|assist|guide|show|teach|explain|tell|list|summarize|analyze|compare|give me|you have|you can|where|review|research|find|draft|compose|extract|process|convert|transform|plan|strategy|approach|method|framework|structure|overview|summary|breakdown|rundown|digest|perspectives|viewpoints|opinions|approaches|angles|pros and cons|advantages and disadvantages|benefits and drawbacks|assuming|suppose|imagine|consider|step by step|procedure|workflow|act as|adapt|prepare|advise|appraise|instruct|prompt|amend|change|advocate|aid|assess|criticise|modify|examine|your|assign|appoint|delegate|nominate|improve|expand|calculate|classify|rank|challenge|check|categorize|order|tag|scan|study|conduct|contradict|update|copy|paste|please|can you|could you|would you|help me|i need|i want|i'm looking for|im looking for|how do i|how can i|what's the|whats the|walk me through|break down|pretend you're|pretend youre|you are a|as a|from the perspective of|in the style of|format this as|write this in|make it|rewrite|i'm trying to|im trying to|i'm struggling with|im struggling with|i have a problem|i'm working on|im working on|what's better|whats better|which|pros and cons of|recommend|suggest|show me how|guide me through|what are the steps|how do i start|whats the process|take me through|outline the procedure|brainstorm|come up with|think of|invent|what if|lets explore|let's explore|help me think|i'm a beginner|im a beginner|as someone who|given that i|in my situation|for my project|i'm currently|im currently|my goal is|depending on|based on|taking into account|considering|given the constraints|with the limitation|improve this|make this better|optimize|refine|polish|enhance|revise|teach me|i want to learn|i don't understand|i dont understand|can you clarify|what does this mean|eli5|i'm confused about|im confused about|also|additionally|furthermore|by the way|who's|whos|find|more|next|also|another|thanks|thank you|please)( [^" "]*){9,}$

Take this strategy with a pinch of salt, as some of these queries might be generated by LLM trackers. 

For instance, I found a pattern of prompts starting with “evaluate,” which have a high number of impressions by zero clicks (not a small number of clicks, exactly zero clicks). If longer prompts have a high number of impressions and no clicks, beware that it might not be humans using these prompts.

Perplexity follow-up questions

One of the main AI Search platforms, Perplexity has a feature called “Related” where it displays up to five follow-up prompts. While the initial prompt is still yours and may not be how others are prompting, the related follow-ups are still a good indicator of how humans prompt—or at least how the platform expects humans would.

These answers are country-specific, so run your research locally.

Semrush AI Visibility Tool

Considering we don’t have the search volume metric per single keyword and that prompts are a lot more unique than keywords, it’s not realistic to track every single prompt relevant to our companies. A way to mitigate this is to combine these prompts into topics and use AI to summarize what they mean.

The new Semrush AI Visibility Tool has a feature called “Prompt Research” that matches your keyword to a topic and gives you a list of prompts alongside brands mentioned, intent, and sources.

Currently, the tool allows you to filter results between the US and the UK, including the full AI Response and a list of brands and URLs. 

Even though I typed a single keyword (“used cars”), it picked the closest available topic (“Used Car Sales and Dealerships”) and returned me all prompts, brand mentions, and source domains.

You might decide not to track single prompts, which can grow fast and become overwhelming to measure. Rather, use the Semrush prompt database for optimization and measure the results by looking at the whole topic performance.

Without grounding, your chances are low

Keep in mind that not every prompt requires RAG, meaning that if the answer is already on the AI Search platform training data, no pages will appear as sources. For some brands, just getting a mention is fine. If, say, someone is looking for a museum or restaurant to visit, the mention might be enough to convince them to reach the destination and convert offline (e.g., buy a ticket or a meal).

In most cases, however, SEOs are still looking for traffic, so the prompt must list pages in their answers to give you a chance to be visible. Ironically, while the results you get from ChatGPT are one answer instead of a SERP, the LLM is actually doing searches for you in the background. 

Luckily, you can find:

• The searches ChatGPT is doing in the background
• The probability of this search requiring a RAG

You can find these by looking for “queries,” “search_queries,” and “search_prob” inside Chrome Dev Tools (Inspect > Network > Conversation > Response).

Or, to simplify, you can add this script as a bookmark on Chrome and click on it after prompting a question on ChatGPT. This is an improved version of Ziggy Shtrosberg’s script.

While these searches look more like traditional searchers as opposed to prompts, your strategy may be to optimize for them and win on AI search as a secondary benefit.

When it comes to search_prob (also on the script above), it’s the probability that an answer requires grounding (RAG). This answer ranges between 0 (low) and 1 (high). Every answer is unique (even if you and I search for the same prompt, we’ll have different answers), so this can act as a proxy for the opportunity of pages being listed as a source.

As with every new technology, things change fast. How people use AI tools and which tools are being used are constantly changing. New models (like ChatGPT5) change how RAG is used, and the increase in adoption across different industries also affects what prompts you should track, so you must also evolve and reevaluate what and how to track AI searches.

See the complete picture of your search visibility.

Track, optimize, and win in Google and AI search from one platform.

Start Free Trial

Get started with

LinkedIn is making Reserved Ads generally available to all managed accounts, giving marketers the ability to lock in the first ad slot in the feed for premium visibility.

What’s new. Reserved Ads let advertisers secure top-of-feed placement at a fixed rate, providing predictable delivery, consistent reach, and greater share of voice. Early results show the format drives up to 75% higher dwell time, 88% higher view-through rates, and delivers 99% of forecasted impressions, according to LinkedIn.

How it works. Reserved Ads appear in the most visible ad slot on LinkedIn’s feed and support most Sponsored Content formats, including Video, Single Image, Carousel, Document, Thought Leader, and Event Ads. Advertisers work with their LinkedIn account representative to reserve inventory and pricing.

Why we care. LinkedIn Reserved Ads give you guaranteed top-of-feed placement, increasing visibility, attention, and engagement for campaigns. This premium positioning helps cut through the typical noise in B2B feeds, improving recall and early-funnel impact.

Additionally, the predictable delivery and fixed pricing allow marketers to plan campaigns with more certainty while building higher-quality retargeting audiences for future conversions.

The big picture. LinkedIn is positioning Reserved Ads as a bridge between brand and demand. By anchoring awareness campaigns at the top of the feed, marketers can build higher-quality retargeting pools — with LinkedIn reporting up to a 101% lift in mid-funnel engagement when audiences are warmed with Reserved Ads ahead of time.

The bottom line. By turning premium feed placement into a reservable product, LinkedIn is giving B2B marketers a more predictable way to buy attention — and convert it into downstream demand.

Google has removed its long-standing unified pricing rules in Google Ad Manager, once again allowing publishers to set different price floors for Google demand versus other programmatic buyers.

What changed. Publishers can now set bidder-specific floor prices in Ad Manager. For example, one buyer can be required to bid at least $5 while others compete at a lower $2 floor. Google has also rebranded “unified pricing rules” as simply “pricing rules.”

The backstory. Before 2019, publishers often set higher floors for Google to counterbalance its data advantage. That flexibility disappeared when Google mandated uniform pricing across exchanges — a move later scrutinized by regulators in both the U.S. and Europe.

Why we care. Bidder-specific pricing rules change how auctions clear and how competitive different demand sources are inside Google Ad Manager. As publishers regain the ability to set higher floors for certain buyers, advertisers may see shifts in win rates, CPMs, and available inventory depending on their buying setup. Over time, this could reshape pricing dynamics and push advertisers to reassess bidding strategies and diversification across exchanges.

Regulatory pressure: The rollback follows major antitrust actions against Google’s ad tech business. In the U.S., Google was found guilty of anti-competitive behavior, prompting proposed remedies that included ending unified pricing. In Europe, the European Commission fined Google €2.95 billion ($3.45 billion) and ordered the company to end self-preferencing practices across the ad tech supply chain.

What Google says: Google said the change will make it easier for publishers and advertisers to use competing ad tech providers while minimizing disruption. The company framed the update as part of broader near-term product changes across display, video, and app ads.

Industry reaction. Jason Kint, CEO of Digital Content Next, called the move a meaningful — if limited — win for publishers, noting that unified pricing often lowered yield and that this change offers immediate, tangible relief. He also suggested the update may be designed to show regulatory compliance and head off stronger remedies, including potential divestitures.

The bottom line. After more than six years, publishers are regaining pricing control inside Google Ad Manager — a shift driven less by product strategy and more by mounting antitrust pressure on Google’s ad tech empire.

Google recently rolled out “read more” links in Google search results, which appear at the end of the snippet’s description. When you click on the read more link, you are anchored down to a specific portion of the web page that you clicked on.

Not all search result snippets include these read more links, but many do.

What it looks like. Here is a screenshot of this in action, but you can probably replicate it for most of your queries now:

Google was testing this, or variations of this,  back in July and now it seems to have been rolled out.

Why we care. These read more links do add an additional eye-catching link to the search result snippets. Hopefully, this leads to encouraging more clicks to websites and no less.

More clicks to websites is a good thing, so hopefully this feature will last.

Google has expanded Product Studio inside Merchant Center, rolling out three new creative features that go beyond its original image generation tool.

What’s new. In addition to image generation, Product Studio now lets merchants animate static product images into short videos using suggested text prompts, a move aimed squarely at short-form ads and social-style creative.

Google has also added one-click background removal to help isolate products and create cleaner, more consistent Shopping visuals.

The third update increases image resolution, allowing advertisers to upscale older or lower-quality assets to meet modern visual standards.

Why we care. Product imagery plays a major role in Shopping performance, but creating and refreshing assets is often slow and resource-heavy. These updates give merchants more ways to produce high-quality visuals quickly — without leaving Merchant Center or relying on design teams.

The big picture. Google continues to embed AI-powered creative tools directly into commerce workflows. By housing animation, editing, and enhancement inside Merchant Center, Google is lowering the barrier to frequent creative testing — a key lever for Shopping and Performance Max campaigns.

What to watch. These tools could significantly speed up asset iteration for advertisers with limited creative resources, especially as Google pushes more video-forward and visually rich ad formats across Search, Shopping, and YouTube.

First seen. This update was spotted by Senior PPC Specialist – Vojtěch Audy

Google today began rolling out Gemini 3 Flash as the default model powering AI Mode in Search worldwide. The upgrade brings faster performance and stronger reasoning to AI-generated search responses, Google said.

Why we care. With AI Mode, Google continues to transition toward an AI-first search approach. More queries could be answered directly in AI Mode, reducing reliance on traditional organic listings. Improved reasoning allows AI Mode to handle comparison and planning tasks, multi-intent searches, and research-style queries.

What’s changing. Gemini 3 Flash now powers AI Mode in Search globally.

• It replaces earlier Flash-class models previously used in AI Mode.
• AI Mode responses now use Gemini 3-level reasoning with lower latency.

Google is also expanding access to Gemini 3 Pro in Search in the U.S.

• Users can now select “Thinking with 3 Pro” in the AI Mode model menu for more in-depth help on complex questions, including dynamic visual layouts and interactive tools generated on the fly.

What AI Mode does. According to Google, AI Mode:

• Breaks complex queries into multiple parts.
• Pulls real-time information and links from across the web.
• Presents answers in structured, visually organized formats.
• Handles multi-step tasks (e.g., trip planning, learning complex topics).

What Google is saying. In a blog post, Tulsee Doshi, senior director, product management, wrote:

Building on the reasoning capabilities of Gemini 3 Pro, AI Mode with Gemini 3 Flash is more powerful at parsing the nuances of your question. It considers each aspect of your query to serve thoughtful, comprehensive responses that are visually digestible — pulling real-time local information and helpful links from across the web. The result effectively combines research with immediate action: you get an intelligently organized breakdown alongside specific recommendations — at the speed of Search.

This shines when tackling complex goals with multiple considerations like trying to plan a last-minute trip or learning complex educational concepts quickly.

Image generation expands in AI Mode. Google also announced expanded access to Nano Banana Pro, its Gemini 3 Pro–powered image generation and editing model, in Search.

• More U.S. users can now create and edit images directly in AI Mode by selecting “Thinking with 3 Pro” and then “Create Images Pro.”
• Users can add visual explainers, diagrams, and infographics alongside AI-generated answers.

Google Search’s Danny Sullivan and John Mueller pushed back again on the idea that brands need a separate AI SEO strategy during the latest Search Off the Record episode.

Sullivan’s point is simple: the acronyms keep changing (GEO, AEO, etc.), but the advice doesn’t: Write for humans, not for ranking systems, whether those systems are traditional search or LLM-powered experiences.

Why we care. As AI search grows, a lot of publishers and SEOs are feeling pressured to try something new. Google’s take: chasing AI tricks can actually backfire and distract you from making content people actually like.

Google says the north star hasn’t moved. Sullivan said Google aims to reward content made for people, not for search algorithms or for LLMs. If you’re already doing that, he said, you’re “ahead” as formats continue to shift.

• If you optimize narrowly for a specific AI system, you risk permanent catch-up as those systems evolve.
• Modern CMS platforms handle much of the old “make your site crawlable” work by default, Mueller added.

Original, authentic, multimodal. Sullivan argued that AI features speed up a reality publishers have faced for years: commodity content is easy to replace. His examples:

• Pages that padded a simple fact like “What time is the Super Bowl?” into a long post eventually lost to direct answers.
• Sites built on predictable, repeatable answers (e.g., word game solutions) are vulnerable when that information is given directly.

What Google wants creators to do:

• Prioritize original value. Bring perspective, expertise, reporting, firsthand experience, or a voice that only you can provide.
• Lean into authenticity. Not “manufactured authentic,” but work grounded in real experience.
• Go multimodal. Sullivan joked that he hates the term, but the point stands. Mix text with images and video, because users search across formats and often prefer video for how-to answers.

Structured data still matters. They also said structured data helps, but it isn’t decisive. Sullivan said it’s not “structured data and you win AI.” It simply supports how systems understand and present content, just as it already does across Search features.

Focus on quality clicks. Google is seeing that traffic from AI formats can arrive more engaged, such as spending more time on-site. His hypothesis is that AI results create better contextual awareness. Users click when they are more confident that the result matches their intent.

• Google’s advice: define and track outcomes that matter to your business, not just raw traffic.
• Clicks alone don’t tell the full story anymore – especially as AI Overviews and conversational results guide users before they ever visit a site.
• Focus on quality clicks and quality conversions over volume (and be clear on what a conversion actually is).
• Sullivan noted that everyone defines “conversion” differently, which makes it hard for Google to surface that kind of value inside Search Console.

About query fan-out. They explained why “I rank in blue links but not in AI Overviews” is a flawed comparison:

• AI features may run multiple related searches behind the scenes. Mueller described it as doing “a whole bunch of searches for you” and then synthesizing the results.
• That means visibility in AI results may not map one-to-one with the exact query a user typed.

Clients still want “the new thing.” Sullivan acknowledged the real-world challenge: Clients still demand “AI optimization” as a separate service.

• He suggested reframing is to present the “same old stuff” as the durable, long-term strategy.
• Position “AI SEO” as monitoring and adapting, not rebuilding everything into a second content system.
• Sullivan said Generative Engine Optimization (GEO) isn’t separate from SEO – it’s a subset of it. SEO has always been about understanding how people look for information and how systems surface it.
• Optimizing for AI answers is conceptually no different from optimizing for local results, voice search, or other formats. The fundamentals still apply.

What to do now, according to Google. Based on the conversation, Google’s “SEO checklist” looks something like this:

• Create human-first, satisfying content.
• Offer original reporting, unique expertise, firsthand experience, and a strong voice.
• Add images or video when they genuinely improve understanding.
• Use structured data where appropriate.
• Optimize for engagement and conversions, not just clicks.

The podcast. Thoughts on SEO & SEO for AI, part 1

Dig deeper:

• Google says doing optimization for AI search is ‘the same’ as doing SEO for traditional search
• Google VP: SEO and AI search optimization have ‘a lot of overlap’
• Google’s Danny Sullivan: ‘Good SEO is good GEO’
• Google says normal SEO works for ranking in AI Overviews and LLMS.txt won’t be used

💾

Google updated its JavaScript SEO best practices document, for the second time this week, this time to clarify canonicalization best practices for JavaScript. In short, Google said “setting the canonical URL to the same URL as in the original HTML or if that isn’t possible, to leave the canonical URL out of the original HTML.”

What Google added. Google added a new section over here and it reads:

“The rel=”canonical” link tag helps Google find the canonical version of a page. You can use JavaScript to set the canonical URL, but keep in mind that you shouldn’t use JavaScript to change the canonical URL to something else than the URL you specified as the canonical URL in the original HTML. The best way to set the canonical URL is to use HTML, but if you have to use JavaScript, make sure that you always set the canonical URL to the same value as the original HTML. If you can’t set the canonical URL in the HTML, then you can use JavaScript to set the canonical URL and leave it out of the original HTML.”

Google on noindex. Google also warned about using JavaScript for noindex tags earlier this week. Google said “you do want the page indexed, don’t use a noindex tag in the original page code.”

Why we care. So if you use JavaScript for setting a canonical link, make sure to also check in Google Search Console’s URL Inspection tool if it is being picked up.

Review these updated best practices if you use JavaScript on your site, especially for canonical links.

For years, PPC advertisers have considered Performance Max (and Smart Shopping before it) to be a black box, even a black hole.

While its powerful automation drives convincing results, the lack of transparency into channel performance has been a persistent frustration. 

Now, Google is beginning to provide some answers. 

The rollout of the new Channel Performance report marks a significant step toward the transparency advertisers have been demanding. 

This guide explains what the report is, highlights its strengths and weaknesses, and shows you how to use it.

What is the Channel Performance report – and why is it a big deal?

The Channel Performance report is essentially a pre-built network report (we can discuss the semantics of channel versus network another day), which can be found under Campaigns > Insights and Reports > Channel Performance (beta).

It offers tabular network data and an interactive flow diagram from impressions down through conversions. 

The Channel Performance report only works for Performance Max campaigns. However, credible clues suggest that this report may support additional campaign types in the future.

This is important because, while Performance Max is (in)famously a “channel soup,” all campaign types are capable of serving across different ad networks within Google’s grasp, and many of them do so by default.

Previously, untangling this mix to see which channels were actually performing was a task left to manual reports or, in the case of PMax, third-party scripts based on guesswork.

The Channel Performance report is Google’s native solution. 

A tour of the Channel Performance report

The report is composed of two main elements: 

• An account-level view that offers a compact summary of each campaign’s channel data (plus some hidden features).
• A campaign-level view that offers a neat but, in my opinion, deeply flawed Sankey diagram, and another data table, more detailed than at the account level. 

Furthermore, there are various customization options, which can be saved as preferred views, and multiple export options.

1. The account-level overview: Channel data in the palm of your hand

The account view is a newer addition to the Channel Performance report, and in some ways my favorite view. 

Previously, when you accessed this report, you’d land on a blank page prompting you to select an individual Performance Max campaign. 

Now, this handy table is the first thing you’ll see.

It has a series of rows for each campaign, nested rows for each channel, and columns for the performance metrics. 

One thing I love is that each nested row has the channel icon next to it. 

Tabular data can sometimes make my eyes cross, but this simple visual aid makes the data much easier to skim.

By default, the campaign rows are sorted alphabetically, and you’ll likely want to sort by something more practical, like impressions, costs, revenue, etc.

After that, you can really leap down the page easily, comparing the distribution of your key campaigns.

But that’s the obvious part.

My top tip for this view is that you can change your segment, and among the options, two really stand out for me: 

• Ads using product data.
• Ad event type (under Segment > Conversions).

The first allows you to see the volume and performance of “ads using product data” (feed-based ads) versus “ads not using product data” (asset-based ads).

Yes, that’s right, finally a simple comparison of feed ads and asset ads. Besides network performance, this has been one of the most contentious and least transparent areas in PMax, prompting numerous advertisers to run so-called “feed-only” PMax campaigns.

Now you can easily see what’s going on with this performance facet across all your PMax campaigns, plus an account-level summary row at the bottom. 

Whether you like or dislike what you’re seeing, you can head over to your asset-group-level and asset-level reporting to dig deeper. 

Be cautious when judging the performance of asset-based ads. They should not be held to the same efficiency standards.

The second segment, ad event type, might sound non-descript, but it’s really important.

It lets you easily understand the volume and performance of your click-through versus view-through conversions. 

This has been (yet another) divisive topic in PMax: 

• Do view-based conversions belong mixed together with standard conversions? 
• Does this inflate performance? 

Now you can answer these questions per campaign and also at the account view in the summary row.

But what if you want even more detail? 

What if, for example, you want to learn your feed versus asset share in, say, YouTube specifically? 

That’s not possible at the account level, but it certainly is at the campaign level.

Just click on any campaign and it will load a new page drilling down to the next reporting level. 

2. The campaign-level view: Data visualization and detailed analysis

The first thing you’ll notice on this page is the large Sankey diagram. 

It’s visually striking and has become a signature of the Channel Performance report.

That said, we need to set it aside for now. Scroll down to the data table below, which is similar to the one you just saw.

The campaign data table: A deeper dive

While the Sankey diagram gives a high-level view, the table below is where real analysis happens. 

It’s more reliable for decision-making because it shows the raw numbers without visual distortion.

The table breaks performance down by channel and ad type – the feed-based versus asset-based split we discussed earlier. 

For each segment, you can review multiple metrics by default, but my top tip is to go to Columns > Conversions.

There, you can select Conv. value / Cost (a.k.a. ROAS) and Cost / Conv. (a.k.a. CPA). 

These are hidden by default, but you can indeed see them, and I don’t think I have to tell you why they are interesting to know.

Crucially, the table also includes an export function, plus scheduling options, allowing you to pull the raw data for deeper analysis in a spreadsheet.

The Sankey diagram: Visualizing the flow

As noted earlier, this visualization – officially called the Channels-to-Goals chart – is visually striking, but it has limitations. 

Before addressing those issues, let’s clarify its purpose and what it can tell us.

The Sankey diagram presents a visual breakdown of performance across the channels within your PMax campaign. 

It maps the customer journey within your campaign – how users move from seeing an ad (impressions) to clicking or engaging with it (interactions), and, ultimately, to converting (results or conversions).

This is great. For the first time, advertisers can see the flow of core funnel metrics right in Google Ads, all segmented by the specific channel driving the traffic. 

This allows you to understand how PMax allocates your budget and which parts of its vast inventory are actually working for you.

Decoding the channels

People often look at the Sankey and get stuck. “Where’s my Shopping data?” is probably the single biggest example of this. 

As we’ve discussed, a key feature of the report is how it segments ads into feed-based and asset-based ads.

When we combine that dimension with the network or “channel” dimension, we can translate the labels into more familiar terms:

• Search
  • Ads using product data: These are your Shopping ads.
  • Other ads: This represents your Dynamic Search Ads (DSA) and Responsive Search Ads (RSA) traffic.
• Display
  • Ads using product data: These are Dynamic Product Ads, which in my assessment is likely a lot of Dynamic Remarketing and some Dynamic Prospecting.
  • Other ads: These are your standard Responsive Display ads.

These are my interpretations of the data, which might not be perfect. 

It would be extremely helpful if Google offered more detailed documentation on what’s included.

For example, feed-based YouTube ads can comprise a variety of formats and placements, some of which, such as “GMC Image Shorts,” are not documented anywhere.

Google’s guidance is quite vague.

---

The limitations of the native report

While a welcome addition, the report has some shortcomings.

The misleading Sankey diagram 

The visual proportions of the diagram are not based on volume, which makes it extremely misleading at a glance. 

A channel that appears to drive significant traffic may actually account for only a tiny share of your impressions.

In the example below, the asset-based Search ads segment appears to have a couple hundred thousand impressions, but in reality only has 4,500 impressions. 

This makes the chart almost useless for quick, accurate analysis, which is the entire point of data visualization.

The lack of ratios in the data table 

The data table provides useful raw data, but it lacks key calculated metrics needed for analysis, such as conversion rate and cost per click.

To see the full picture, you must export the data and do your own calculations.

This feels, to be honest, a bit petty of Google. 

They could easily add these columns, but it seems they would prefer not to. Grab your calculator.

How to make the most of the report

Despite its limitations, you can still extract valuable insights into which channels deliver what.

The key is to focus on asset quality and traffic quality, because direct channel control is limited.

Analyze placement data for quality control 

While the report doesn’t let you directly control channel mix, it helps you monitor traffic quality. 

Use the placement reports to see exactly where your Display and YouTube ads are showing.

• Export this data into Google Sheets. Note that, frustratingly, it only contains impression data.
• Use built-in functions like =GOOGLETRANSLATE() to understand foreign-language placements and the integrated =AI() function to help categorize domains and videos for brand safety.
• Exclude low-quality or irrelevant placements or content at the account level, prioritizing bad placements that are higher in volume.

Build your own Sheets-based reporting or try scripts

Google has confirmed that API access and MCC-level reporting are coming to the Channel Performance report. I also expect this data to be supported in the Report Editor. 

In the meantime, you can export the report as a .csv or send it directly to Google Sheets.

With a smart setup, these exports enable you to calculate custom metrics, build charts, apply heatmaps, and reshape the data as needed.

To help the community, I helped build a script that enhances Google’s report in several practical ways:

• Adds key metrics like conversion rate, CTR, CPC, CPM, and more.
• Applies clear, common-sense labels such as “Shopping” and “Responsive Display.”
• Includes charts with proportional visuals for more accurate interpretation.
• Cleans and parses columns to remove friction.

The script works for individual PMax campaigns, not the account-level view. I’m waiting for Google’s feature set and scripting options to stabilize before expanding the script.

What’s next for PMax reporting?

We know Search Partner data is coming, along with API access, MCC-level reporting, and likely support for additional campaign types such as Demand Gen.

It’s encouraging to see Google share this level of detail, and there’s reason to believe this momentum will continue. 

The Channel Performance report already addresses one of the most persistent criticisms of Performance Max – that it operates as a black box. 

Three years ago, it would have been hard to imagine Google responding to advertiser feedback at this scale, particularly on transparency.

Still, better visibility doesn’t automatically translate into better decisions. 

Interpreting this data correctly takes time, context, and careful analysis – and that work remains firmly in the hands of advertisers.

Microsoft Copilot is transforming search advertising by turning everyday conversations into intent-rich signals advertisers can act on. 

ROAS increases 13-fold when users engage with Copilot before performing a search, according to Microsoft.

Drawing from billions of first-party audience insights across Microsoft’s consumer ecosystem – including Bing, Edge, Xbox, LinkedIn, and Activision – Copilot identifies high-value audiences using deterministic data built from search intent, web activity, and profile information. 

This allows advertisers to reduce wasted impressions and stretch budgets further.

The mechanics of intent-rich search 

The core proposition of conversational search is that users provide significantly more context to a chatbot than to a traditional search bar. 

Instead of a fragmented keyword, users are increasingly asking detailed questions.

When a user submits a complex query – such as asking for specific product comparisons or local recommendations – the AI triggers multiple backend searches across reviews, specifications, and availability to construct an answer. 

For the advertising industry, this behavior change offers a potential goldmine of data. 

By interpreting these longer queries, platforms can identify “high-intent” buyers more accurately, turning a single conversation into multiple, precise ad opportunities.

Applying conversational intent to a real-world campaign

To understand how these metrics translate into strategy, consider a recent test I conducted for a well-known California-based university tasked with recruiting high school seniors for their hands-on engineering and architecture STEM programs.

The challenge

The university historically relied on broad keywords like “best engineering schools.”

This resulted in high competition and wasted spend on students looking for art programs or out-of-state options they couldn’t afford.

The conversational approach

Using Copilot’s intent signals, the campaign shifts.

A prospective student might ask Copilot:

• “Find me a university with a strong robotics program, under $30,000 tuition, located on the West Coast.”

The results

Applying Microsoft’s reported benchmarks to this scenario reveals significant efficiency gains:

• Slashed waste: The university realizes a 32% reduction in wasted impressions because ads are not shown to students whose conversational context indicates irrelevant intent.
• Budget efficiency: By targeting intent rather than broad volume, the campaign drives a 48% decrease in cost per acquisition (CPA) compared to search alone.
• Higher engagement: Because the ad appears as a helpful solution to a specific question, engagement lifts by 153%.

Action plan: Transitioning to intent-based advertising 

For advertisers seeking to replicate these results, the shift necessitates more than simply enabling a new setting. 

It requires a strategic overhaul of how campaigns are structured to capture “conversational” demand.

Phase 1: Foundation and data (The signal layer)

Audit service offerings and solution data

Ensure your site’s structured data is rich with details on specific methodologies and industry specializations. 

AI assistants rely on this semantic depth to answer prospective queries about “competency, case studies, and communication options.”

Prioritize first-party data

Integrate customer data to train the model. 

Microsoft’s ecosystem leverages data points from LinkedIn to Xbox to refine targeting.

Advertisers must supply their own truth data to match this precision.

Phase 2: Campaign structure (The capture layer)

Embrace long-tail queries

Move away from strict exact-match keywords.

The UI overhaul of Copilot encourages users to ask “longer, more detailed questions,” meaning broad match modifiers are necessary to capture these natural language phrases.

Optimize for answers, not just clicks

Structure landing page content to answer specific questions. 

Since Copilot acts as a “companion” guiding users through tasks, your ad content must align with helping them make a decision, not just selling a product.

Phase 3: Cross-channel integration (The scale layer)

Implement cross-device strategy

With 90% of Gen Z adults in the U.S. using the web while watching TV, campaigns must run across multiple platforms, including mobile, PC, and console, to capture their split focus.

Bridge the authenticity gap

For younger demographics, leverage integrations like Snapchat’s My AI. 

This places ads within “conversational flows” rather than interrupting them, a key factor in engaging Gen Z.

---

The Gen Z challenge: Authenticity vs. algorithms 

Bridging the gap with Gen Z remains a hurdle for most ad platforms, which often struggle with perceptions of inauthenticity. 

To address this, the industry is seeing a trend toward utilizing behavioral data from unlikely sources. 

By layering in data from gaming ecosystems like Activision, advertisers can target based on real behaviors – from play styles to in-game purchases – ensuring campaigns feel relevant rather than generic.

To legitimize whether Copilot is effectively targeting Gen Z – or just efficiently automating ad delivery – we must look beyond corporate claims. 

Microsoft’s strategy relies on a “closed loop” of gaming data, social integration, and conversational signals.

Does this actually work for a generation that is famously resistant to traditional advertising? 

The answer lies in the tension between utility and authenticity.

The behavioral match

Microsoft’s claim that Copilot “cracks the code” is mechanically sound because it aligns with how Gen Z actually searches.

The shift from keywords to conversation

Data shows that Gen Z users write the longest search queries (avg. 5.83 words) and are the most likely to use complete sentences.

They treat search engines like companions, asking “What is the best…” rather than typing “best shoes NYC.”

Legitimacy verdict: High. Copilot isn’t trying to force a behavior change. It is capitalizing on one that already exists.

By decoding these long, conversational queries, Microsoft captures intent often missed by a keyword approach alone.

‘Gaming data’ targeting 

Using Activision data to target users based on “play styles” is a strong differentiator for Microsoft.

The reality: 90% of Gen Z second-screens (uses a phone while watching/playing on another screen). Traditional demographics (e.g., “Male, 18-24”) are failing because they are too broad.

The legitimacy test: Targeting a user because they play Overwatch (identifying them as team-oriented and strategic) vs. Call of Duty (identifying them as reactive and fast-paced) allows for psychographic targeting that feels “relevant” rather than “intrusive.”

The risk is that there is a fine line between “relevant” and “stalker-ish.” 

While Microsoft’s targeting is effective, 76% of Gen Z actively avoid ads, and privacy concerns are their top barrier to trusting AI platforms. 

That said, the success of this strategy hinges on the ads feeling native to the experience, not like data extraction.

The authenticity paradox

This is the weak point in the strategy. Microsoft claims Copilot helps bridge the “authenticity gap,” but Gen Z is inherently skeptical of AI-generated content.

The conflict: Studies show that Gen Z can easily identify AI-generated ads and often labels them as “annoying” or “boring” compared to human-created content.

The Snap integration: Embedding Copilot ads into Snapchat’s “My AI” is a double-edged sword. While it places ads in a trusted social space, it risks polluting a private sanctuary. 

If “My AI” starts feeling like a corporate shill, users may abandon the feature entirely.

Legitimacy is mixed. The placement is correct (Snapchat, Games), but the content is at risk. 

If advertisers use Copilot to auto-generate generic ad copy, it will fail. Success requires using the AI for targeting but keeping the creative 100% human.

The verdict: Is Microsoft effectively targeting Gen Z?

• Technically: Yes, they have successfully built a mousetrap that catches Gen Z where they live (gaming, social, conversational search).
• Culturally: To be determined. The efficiency is there (lower CPA, higher ROAS), but “legitimizing” the strategy long-term requires overcoming the “uncanny valley” of AI trust.

Dig deeper: How Gen Z is redefining discovery on TikTok, Pinterest, and beyond

A new economic reality 

The narrative from platforms like Microsoft Copilot is that AI-driven targeting creates a “closed loop” where better engagement drives cost savings. 

As conversational AI reshapes how consumers interact with the web, advertising platforms are racing to translate natural language questions into actionable intent. 

Microsoft’s Copilot serves as a prime case study of this shift, demonstrating how emerging assistants generate richer, multi-step queries that potentially reshape search economics from a volume game to one of precision.

For advertisers, this signals a fundamental transition: moving away from the broad “spray and pray” tactics of keyword volume toward a model where conversational signals drive ROAS.

Dig deeper: The future of remarketing? Microsoft bets on impressions, not clicks

Why this matters now

Marketing budgets in 2025 have stayed the same, yet expectations keep rising. CMOs report budgets stuck at roughly 7.7% of company revenue, which means teams are expected to do more with the same dollars. In that context, the most practical use of AI is not a moonshot, but a set of clear fixes to everyday bottlenecks that slow teams down and drive costs up.

This article breaks down four problems that marketers face right now and how AI is already solving them. The difference today is that Artlist AI, including image, video and voice generators, turns AI from a novelty into a reliable production system. When you use AI to streamline your workflow instead of chasing hype, you ship more creative, stay on brand and make decisions based on real performance data. 

1) Rising video costs and shrinking timelines

The problem: Video is still one of the most effective formats in a marketer’s toolkit, but teams feel the squeeze. Shorter formats dominate social feeds, content calendars never stop  and production bottlenecks turn into budget overruns. Teams need more output in less time. 

What’s working: Marketers still see strong returns from video. Wyzowl’s 2024 study reports 90% of marketers say video delivers a good ROI, with 30–60 seconds rated the most effective length, perfect for social placements and paid tests. That supports a strategy shift that marketers need to ship more short pieces, produced in cycles measured in days instead of weeks.

How AI helps:

This is exactly where Artlist AI leads. It helps teams to finish videos in hours not weeks, giving you more room to test, refine, and scale video output without sacrificing quality

• Script to screen speed. Artlist AI storyboards, image generation and AI video generation help teams audition more concepts in less time, then move proven ideas into full production.
  
• On-the-fly variations. Once a master edit is locked, AI tools can generate multiple aspect ratios and quick alternates for A/B testing without re-editing from scratch.
  
• Voiceover without the studio. High-quality Artlist AI voiceover makes late-stage copy changes effortless, eliminating the need for booth bookings or talent scheduling. And brands can easily keep tone and pacing consistent.

Klarna recently publicly quantified its savings: about $10 million annually tied to AI in marketing, including a $6 million reduction in image production costs and much faster iteration cycles. While every team’s baseline differs, the directional takeaway is strong and indicates that small time wins across dozens of workstreams add up to real money. 

2) Inconsistent brand voice across markets and channels

The problem: Global campaigns require many voices, languages and platform variations. Human recording sessions can create drift in tone and pacing, and late edits become expensive.

What’s working: Studio-grade text to speech models and voice cloning technology now produce narration that is indistinguishable from a human voice, even when using headphones. This makes versioning practical at scale while keeping quality consistent across dozens of outputs.

How AI helps:

Artlist’s AI voiceover gives you one brand voice you can trust, every time, across every market. 

• Stable tone across languages. A single brand voice can be replicated across scripts and regions, then fine-tuned for pacing, warmth, and energy. This is made easy with Artlist’s voice cloning models.
  
• Rapid revisions. Late copy changes are possible at sensible price points, covered by legal licenses and mean details such as new promotion dates can be updated in minutes, not weeks, with less stress on marketers.
  
• Accessible variants. AI voice and caption pipelines support business localization efforts and accessible workflows without extra studio time. Global campaigns often stall when localized content is linguistically inconsistent. Translation alone doesn’t guarantee cultural fit, and recreating dozens of regional versions drains budgets. AI translation and dubbing tools are closing the gap between literal accuracy, cultural fluency, and still retain the emotion marketers aim for. 

airBaltic, the national airline of Latvia, uses Artlist’s AI voiceover to speed production and experiment with tone and pacing, reporting that work that used to take many hours now moves much faster, with tighter control over fit and finish before publication. For a team managing constant route and fare updates, shaving hours off every revision adds meaningful capacity.

3) Creative testing at the speed of social

The problem: Marketers know more than most how feeds change daily. What worked last quarter may stall today. Marketers need more creative swings, which means more thumbnails, cuts, and captions, all without blowing the budget.

What’s working: Recent data points to one clear advantage: brands that test creative variations more frequently outperform those that don’t. A 2024 Nielsen study found that campaigns using three or more creative versions improved ad recall by up to 32%, while those refreshing assets monthly saw 17% higher click-through rates than static campaigns. 

AI tools now make A/B testing much easier. Whether the changes are big or small, they are much less taxing, and keeping up with the increased cadence is possible by producing and refining short-form assets in hours instead of days. AI tools like video generators allow marketers to generate alternate visuals, swap voiceovers or localize content without requiring new studio sessions.

In 2023, Coca-Cola invited consumers to produce artwork and short videos using AI trained on its licensed brand assets. Within the first week, participants generated over 100,000 original pieces, driving more than 30% higher digital engagement that quarter. Internally, the company’s marketing team analyzed those submissions to understand which visuals and tones drew the strongest responses. That feedback reshaped future campaign planning, trimming production time and improving message precision.

How AI helps:

Artlist AI lets you scale creative volume without scaling your budget, so you can test and learn faster. 

• Images and thumbnails at scale. Rapid asset generation means marketers can refresh visuals for each social cycle without starting from zero.
  
• Micro-edits for micro-audiences. Teams can test small creative differences — intro clips, CTAs or captions — against audience segments and measure results quickly.
  
• Faster learning loops. Instead of waiting for quarterly reports, marketers can identify high-performing creative in real time and reallocate spend to proven variants.

Creative volume matters less than creative velocity. When teams can produce, test, and iterate at social speed, they turn marketing from a guessing game into a measured system of learning.

4) Measuring creative impact with real feedback loops

The problem: Marketers still rely heavily on vanity metrics, for example, views, likes and impressions, but they say little about actual persuasion. Traditional testing cycles are slow, and connecting creative choices to downstream results is often guesswork.

What’s working: AI analytics tools can now correlate creative elements like color palettes, pacing, tone or voice style, with engagement and conversion metrics. Instead of waiting for a quarterly attribution report, teams can see which versions perform best in near real time.

In 2024, Mondelez used AI-based video analysis to study over 12,000 ad variants across brands like Oreo and Cadbury. The company found that ads with warmer narration tones and moderate pacing drove 19% higher recall and 11% stronger purchase intent. Those insights were rolled back into production templates, improving both speed and consistency across markets. Mondelez also recently disclosed plans to reduce production costs by 30–50% using its generative-AI tool, with an investment of over U.S. $40 million and target rollout of AI-generated TV ads by the 2026 holiday season.

How AI helps:

• Content analysis at scale. Vision and audio models scan thousands of creative variants to detect which stylistic traits correlate with stronger brand recall.
  
• Real-time dashboards. Campaign teams get immediate feedback on performance by geography, audience, or platform instead of waiting for end-of-month reports.
  
• Creative optimization guidance. AI tools surface which combinations of voice, script length, or visual tone work best, turning subjective preferences into measurable variables.

For the first time, creative decisions such as voice choice, image framing and script tempo can be validated by behavioral data, not just opinion. That feedback loop helps marketers spend smarter and produce more resonant campaigns.

The takeaway

Marketers don’t need a grand reset to benefit from AI. The immediate wins are practical: faster video, full production cycles, steady brand voice across regions, more creative tests per month, tighter compliance and a relieved creative team. In a year when budgets are steady rather than expanding, those gains matter. The smartest teams ship smaller, learn quicker and document everything, turning AI from a headline into a dependable part of how they make and run campaigns. 

If you’re ready to modernize your workflow and unlock real creative speed, talk to Artlist’s experts. Join 33 million creators using Artlist to produce high-volume, studio-level content without the studio cost, and see how Artlist AI can transform the way you work. 

Ginny Marvin, Google’s Ads Liaison, is clarifying how keyword match types interact with AI Overviews (AIO) and AI Mode ad placements — addressing ongoing confusion among advertisers testing AI Max and mixed match-type setups.

Why we care. As ads expand into AI-powered placements, advertisers need to understand which keywords are eligible to serve — and when — to avoid unintentionally blocking reach or misreading performance.

Back in May. Responding to questions from Marketing Director Yoav Eitani, Marvin confirmed that an ad can serve either above or below an AI Overview or within the AI Overview — but not both in the same auction:

• “Your ad could trigger to show either above/below AIO or within AIO, but not both at this time.” Marvin confirmed.

While both exact and broad match keywords can be eligible to trigger ads above or below AIO, only broad match keywords (or keywordless targeting) are eligible to trigger ads within AI Overviews.

What’s changed. In a follow-up exchange with Paid Search specialist Toan Tran, Marvin clarified that Google has updated how eligibility works. Previously, the presence of an exact match keyword could prevent a broad match keyword from serving in AI Overviews. That is no longer the case.

• “The presence of the same keyword in exact match will not prevent the broad match keyword from triggering an ad in an AI Overview, since the exact match keyword is not eligible to show Ads in AI Overviews and hence not competing with the broad match keyword.” Marvin said.

Since exact and phrase match keywords are not eligible for AI Overview placements, they do not compete with broad match keywords in that auction — meaning broad match can still trigger ads within AIO even when the same keyword exists as exact match.

The big picture. Google is reinforcing a clear separation between traditional keyword matching and AI-powered intent matching. Ads in AI Overviews rely on a deeper understanding of both the user query and the AI-generated content, which is why eligibility is limited to broader targeting signals.

The bottom line. Exact and phrase match keywords won’t show ads in AI Overviews — but they also won’t block broad match from doing so. For advertisers leaning into AI Max and AIO placements, broad match and keywordless strategies are now essential to unlocking reach in Google’s AI-driven surfaces.

Google rapidly expanded AI Overviews in search during 2025, then pulled back as they moved into commercial and navigational queries. These findings are based on a new Semrush analysis of more than 10 million keywords from January to November.

AI Overviews surged, then retreated. Google didn’t roll out AI Overviews in a straight line in 2025. A mid-year spike gave way to a pullback, suggesting Google moved fast to test the feature, then eased off based on user data:

• January: 6.5% of queries triggered an AI Overview
• July: AI Overview visibility peaked, appearing in just under 25% of queries.
• November: Coverage fell back to less than 16% of queries.

Zero-click behavior defied expectations. Surprisingly, click-through rates for keywords with AI Overviews have steadily risen since January. AI Overviews don’t automatically reduce clicks and may even encourage them.

• AI Overviews still appear more often on searches that already tend to drive no clicks.
• But when Semrush compared the same keywords before and after an AI Overview appeared, zero-click rates fell from 33.75% to 31.53%.

Informational queries no longer dominate. Early 2025 AI Overviews were almost entirely informational:

• January: 91% informational
• October: 57% informational

Now, AI Overviews are appearing for commercial and transactional queries:

• Commercial queries: Increased from 8% to 18%
• Transactional queries: Increased from 2% to 14%

Navigational queries are rising fast. In an unexpected shift, AI summaries are increasingly intercepting brand and destination searches:

• Navigational AI Overviews grew from under 1% in January to more than 10% by November.

Google Ads + AI Overviews. Earlier this year, ads rarely appeared next to AI Overviews. Now they’re common:

• Ads alongside AI Overviews rose from about 3% in January to roughly 40% by November.
• Ads show at the bottom of around 25% of AI Overview SERPs.

Science is the most impacted industry. By keyword saturation, Science leads all verticals for AI Overviews at 25.96%. Computers & Electronics follows at 17.92%, with People & Society close behind at 17.29%.

• Since March, Food & Drink has seen the fastest growth in AI Overviews of any category.
• Meanwhile, Real Estate, Shopping, and Arts & Entertainment remain lightly affected, with AI Overviews appearing on fewer than 3% of keywords.

Why we care. AI Overviews are unevenly and persistently reshaping click behavior, commercial visibility, and ad placement. Volatility is likely to continue, so closely monitor performance shifts tied to AI Overviews.

The report. Semrush AI Overviews Study: What 2025 SEO Data Tells Us About Google’s Search Shift

Dig deeper. In May, I reported on the original version of Semrush’s study in Google AI Overviews now show on 13% of searches: Study.

We are navigating the “search everywhere” revolution – a disruptive shift driven by generative AI and large language models (LLMs) that is reshaping the relationship between brands, consumers, and search engines.

For the last two decades, the digital economy ran on a simple exchange: content for clicks. 

With the rise of zero-click experiences, AI Overviews, and assistant-led research, that exchange is breaking down.

AI now synthesizes answers directly on the SERP, often satisfying intent without a visit to a website. 

Platforms such as Gemini and ChatGPT are fundamentally changing how information is discovered. 

For enterprises, visibility increasingly depends on whether content is recognized as authoritative by both search engines and AI systems.

That shift introduces a new goal – to become the source that AI cites.

A content knowledge graph is essential to achieving that goal. 

By leveraging structured data and entity SEO, brands can build a semantic data layer that enables AI to accurately interpret their entities and relationships, ensuring continued discoverability in this evolving economy.

This article explores:

• The difference between traditional search and AI search, including the concept of comprehension budget.
• Why schema and entity optimization are foundational to discovery in AI search.
• The content knowledge graph and the importance of organizational entity lineage.
• The enterprise entity optimization playbook and deployment checklist.
• The role of schema in the agentic web.
• How connected journeys improve customer discovery and total cost of ownership.

The fundamental difference between traditional and AI search

To become a source that AI cites, it’s essential to understand how traditional search differs from AI-driven search.

Traditional search functioned much like software as a service. 

It was deterministic, following fixed, rule-based logic and producing the same output for the same input every time.

AI search is probabilistic. 

It generates responses based on patterns and likelihoods, which means results can vary from one query to the next. 

Even with multimodal content, AI converts text, images, and audio into numerical representations that capture meaning and relationships rather than exact matches.

For AI to cite your content, you need a strong data layer combined with context engineering – structuring and optimizing information so AI can interpret it as reliable and trustworthy for a given query.

As AI systems rely increasingly on large-scale inference rather than keyword-driven indexing, a new reality has emerged: the cost of comprehension. 

Each time an AI model interprets text, resolves ambiguity, or infers relationships between entities, it consumes GPU cycles, increasing already significant computing costs.

A comprehension budget is the finite allocation of compute that determines whether content is worth the effort for an AI system to understand.

4 foundational elements for AI discovery

For content to be cited by AI, it must first be discovered and understood. 

While many discovery requirements overlap with traditional search, key differences emerge in how AI systems process and evaluate content.

1. Technical foundation

Your site’s infrastructure must allow AI engines to crawl and access content efficiently. 

With limited compute and a finite comprehension budget, platform architecture matters. 

Enterprises should support progressive crawling of fresh content through IndexNow integration to optimize that budget.

Ideally, this capability is native to the platform and CMS.

2. Helpful content

Before creating content, you need an entity strategy that accurately and comprehensively represents your brand. 

Content should meet audience needs and answer their questions. 

Structuring content around customer intent, presenting it in clear “chunks,” and keeping it fresh are all important considerations.

Dig deeper: Chunk, cite, clarify, build: A content framework for AI search

3. Entity optimization

Schema markup, clean information architecture, consistent headings, and clear entity relationships help AI engines understand both individual pages and how multiple pieces of content relate to one another. 

Rather than forcing models to infer what a page is about, who it applies to, or how information connects, businesses make those relationships explicit.

4. Authority

AI engines, like traditional search engines, prioritize authoritative content from trusted sources. 

Establishing topical authority is essential. For location-based businesses, local relevance and authority are also critical to becoming a trusted source.

The myth: Schema doesn’t work

Many enterprises claim to use schema but see no measurable lift, leading to the belief that schema doesn’t work. 

The reality is that most failures stem from basic implementations or schema deployed with errors.

Tags such as Organization or Breadcrumb are foundational, but they provide limited insight into a business. 

Used in isolation, they create disconnected data points rather than a cohesive story AI can interpret.

The content knowledge graph: Telling AI your story

The more AI knows about your business, the better it can cite it. 

A content knowledge graph is a structured map of entities and their relationships, providing reliable information about your business to AI systems.

Deep nested schema plays a central role in building this graph.

A deep nested schema architecture expresses the full entity lineage of a business in a machine-readable form.

In resource description framework (RDF) terms, AI systems need to understand that:

• An organization creates a brand.
• The brand manufactures a product.
• The product belongs to a category.
• Each category serves a specific purpose or use case.

By fully nesting entities – Organization → Brand → Product → Offer → PriceSpecification → Review → Person – you publish a closed-loop content knowledge graph that models your business with precision.

Dig deeper: 8 steps to a successful entity-first strategy for SEO and content

---

The enterprise entity optimization playbook

In “How to deploy advanced schema at scale,” I outlined the full process for effective schema deployment – from developing an entity strategy through deployment, maintenance, and measurement.

Automating for operational excellence

At the enterprise level, facts change constantly, including product specifications, availability, categories, reviews, offers, and prices. 

If structured data, entity lineage, and topic clusters do not update dynamically to reflect these changes, AI systems begin to detect inconsistencies.

In an AI-driven ecosystem where accuracy, coherence, and consistency determine inclusion, even small discrepancies can erode trust.

Manual schema management is not sustainable.

The only scalable approach is automation – using a schema management solution aligned with your entity strategy and integrated into your discovery and marketing flywheel.

Measuring success: KPIs for the generative AI era

As keyword rankings lose relevance and traffic declines, you need new KPIs to evaluate performance in AI search.

• Brand visibility: Is your brand appearing in AI search results?
• Brand sentiment: When your brand is cited, is the sentiment positive, negative, or neutral?
• LLM visibility: Beyond branded queries, how does your performance on non-branded terms compare with competitors?
• Conversions: At the bottom of the funnel, are conversion metrics being tracked and optimized?

Dig deeper: 7 focus areas as AI transforms search and the customer journey in 2026

From reading to acting: Preparing for the agentic web

The web is shifting from a “read” model to an “act” model.

AI agents will increasingly execute tasks on behalf of users, such as booking appointments, reserving tables, or comparing specifications.

To be discovered by these agents, brands must make their capabilities machine-callable. Key steps to prepare include:

• Create a schema layer: Define entity lineage and executable capabilities in a machine-readable format so agents can act on your behalf.
• Use action vocabularies: Leverage Schema.org action vocabularies to provide semantic meaning and define agent capabilities, including:
  • ReserveAction.
  • BookAction.
  • CommunicateAction.
  • PotentialAction.
• Establish guardrails: Declare engagement rules, required inputs, authentication, and success or failure semantics in a structured format that machines can interpret.

Brands that are callable are the ones that will be found. Acting early provides a compounding advantage by shaping the standards agents learn first.

The enterprise entity deployment checklist

Use this checklist to evaluate whether your entity strategy is operational, scalable, and aligned with AI discovery requirements.

• Entity audit: Have you defined your core entities and validated the facts?
• Deep nesting: Does your JSON-LD reflect your business ontology, or is it flat?
• Authority linking: Are you using sameAs to connect entities to Wikidata and the Knowledge Graph?
• Actionable schema: Have you implemented PotentialAction for the agentic web?
• Automation: Do you have a system in place to prevent schema drift?
• Single source of truth (SSOT): Is schema synchronized across your CMS, GBP, and internal systems?
• Technical SEO: Are the technical foundations in place to support an effective entity strategy?
• IndexNow: Are you enabling progressive and rapid indexing of fresh content?

Connected customer journeys and total cost of ownership

Your martech stack must align with the evolving customer discovery journey. 

This requires a shift from treating schema as a point solution for visibility to managing a holistic presence with total cost of ownership in mind.

Data is the foundation of any composable architecture. 

A centralized data repository connects technologies, enables seamless flow, breaks down departmental silos, and optimizes cost of ownership.

This reduces redundancy and improves the consistency and accuracy AI systems expect.

When schema is treated as a point solution, content changes can break not only schema deployment but the entire entity lineage. 

Fixing individual tags does not restore performance. Instead, multiple teams – SEO, content, IT, and analytics – are pulled into investigations, increasing cost and inefficiency.

The solution is to integrate schema markup directly into brand and entity strategy.

When structured content changes, it should be:

• Revalidated against the organization’s entity lineage.
• Dynamically redeployed.
• Pushed for progressive indexing through IndexNow.

This enables faster recovery and lower compute overhead.

Integrating schema into your entity lineage and discovery flywheel helps optimize total cost of ownership while maximizing efficiency.

A strategic blueprint for AI readiness

Several core requirements define AI readiness.

• Data: Centralized, unified, consistent, and reliable data aligned to customer intent is the foundation of any AI strategy.
• Connected journeys and composable architecture: When data is unified and structured with schema, customer journeys can be connected across channels. A composable martech stack enables consistent, personalized experiences at every touchpoint.
• Structured content: Define organizational entity lineage and create a semantic layer that makes content machine- and agent-ready.
• Distribution: Break down silos and move from channel-specific tactics to an omnichannel strategy, supported by a centralized data source and progressive crawling of fresh content.

Together, these efforts make your omnichannel strategy more durable while reducing total cost of ownership across the technology stack.

Thanks to Bill Hunt and Tushar Prabhu for their contributions to this article.

Google’s pitch for AI-powered bidding is seductive.

Feed the algorithm your conversion data, set a target, and let it optimize your campaigns while you focus on strategy. 

Machine learning will handle the rest.

What Google doesn’t emphasize is that its algorithms optimize for Google’s goals, not necessarily yours. 

In 2026, as Smart Bidding becomes more opaque and Performance Max absorbs more campaign types, knowing when to guide the algorithm – and when to override it – has become a defining skill that separates average PPC managers from exceptional ones.

AI bidding can deliver spectacular results, but it can also quietly destroy profitable campaigns by chasing volume at the expense of efficiency. 

The difference is not the technology. It is knowing when the algorithm needs direction, tighter constraints, or a full override.

This article explains:

• How AI bidding actually works.
• The warning signs that it is failing.
• The strategic intervention points where human judgment still outperforms machine learning.

How AI bidding actually works – and what Google doesn’t tell you

Smart Bidding comes in several strategies, including:

• Target CPA.
• Target ROAS.
• Maximize Conversions.
• Maximize Conversion Value.

Each uses machine learning to predict the likelihood of a conversion and adjust bids in real time based on contextual signals.

The algorithm analyzes hundreds of signals at auction time, such as:

• Device type.
• Location.
• Time of day.
• Browser.
• Operating system.
• Audience membership.
• Remarketing lists.
• Past site interactions.
• Search query.

It compares these signals with historical conversion data to calculate an optimal bid for each auction.

During the “learning period,” typically seven to 14 days, the algorithm explores the bid landscape, testing bid levels to understand the conversion probability curve. 

Google recommends patience during this phase, and in general, that advice holds. The algorithm needs data.

The first problem is that learning periods are not always temporary. 

Some campaigns get stuck in perpetual learning and never achieve stable performance.

Dig deeper: When to trust Google Ads AI and when you shouldn’t

Google’s optimization goals vs. your business goals

The algorithm optimizes for metrics that drive Google’s revenue, not necessarily your profitability.

When a Target ROAS of 400% is set, the algorithm interprets that as “maximize total conversion value while maintaining a 400% average ROAS.” 

Notice the word “maximize.”

The system is designed to spend the full budget and, ideally, encourage increases over time. 

More spend means more revenue for Google.

Business goals are often different. 

You may want a 400% ROAS with a specific volume threshold. 

You may need to maintain margin requirements that vary by product line. 

Or you may prefer a 500% ROAS at lower volume because fulfillment capacity is constrained.

The algorithm does not understand this context. 

It sees a ROAS target and optimizes accordingly, often pushing volume at the expense of efficiency once the target is reached.

This pattern is common. An algorithm increases spend by 40% to deliver 15% more conversions at the target ROAS. Technically, it succeeds. 

In practice, cash flow cannot support the higher ad spend, even at the same efficiency. 

The algorithm does not account for working capital constraints.

Key signals the algorithm can’t understand

AI bidding works well, but it has limits. 

Without intervention, several factors can’t be fully accounted for.

Seasonal patterns not yet reflected in historical data

Launch a campaign in October, and the algorithm has no visibility into a December peak season.

It optimizes based on October performance until December data proves otherwise, often missing early seasonal demand.

Product margin differences

A $100 sale of Product A with a 60% margin and a $100 sale of Product B with a 15% margin look identical to the algorithm. 

Both register as $100 conversions. The business impact, however, is very different. 

This is where profit tracking, profit bidding, and margin-based segmentation matter.

Customer lifetime value variations

Unless lifetime value modeling is explicitly built into conversion values, the algorithm treats a first-time customer the same as a repeat buyer. 

In most accounts, that modeling does not exist.

Market and competitive changes

When a competitor launches an aggressive promotion or a new entrant appears, the algorithm continues bidding based on historical conditions until performance degrades enough to force adjustment. 

Market share is often lost during that lag.

Inventory and supply chain constraints

If a best-selling product is out of stock for two weeks, the algorithm may continue bidding aggressively on related searches because of past performance. 

The result is paid traffic that cannot convert.

This is not a criticism of the technology. It’s a reminder that the algorithm optimizes only within the data and parameters provided. 

When those inputs fail to reflect business reality, optimization may be mathematically correct but strategically wrong.

Warning signs your AI bidding strategy is failing

The perpetual learning phase

Learning periods are normal. Extended learning periods are red flags.

If your campaign shows a “Learning” status for more than two weeks, something is broken. 

Common causes include:

• Insufficient conversion volume – the algorithm typically needs at least 30 to 50 conversions per month.
• Frequent changes that reset the learning period.
• Unstable performance with wide day-to-day fluctuations.

When to intervene

If learning extends beyond three weeks, either:

• Increase the budget to accelerate data collection.
• Loosen the target to allow more conversions.
• Or switch to a less aggressive bid strategy like Enhanced CPC. 

Sometimes the algorithm is simply telling you it does not have enough data to succeed.

Budget pacing issues

Healthy AI bidding campaigns show relatively smooth budget pacing. 

Daily spend fluctuates, but it stays within reasonable bounds. 

Problematic patterns include:

• Front-loaded spending – 80% of the daily budget gone by 10 a.m.
• Consistent underspending, such as averaging 60% of budget per day.
• Volatile day-to-day swings, like spending $800 one day, $200 the next, then $650 after that.

Budget pacing is a proxy for algorithm confidence. 

Smooth pacing suggests the system understands your conversion landscape. 

Erratic pacing usually means it is guessing.

The efficiency cliff

This is the most dangerous pattern. Performance starts strong, then gradually or suddenly deteriorates.

This shows up often in Target ROAS campaigns. 

• Month 1: 450% ROAS, excellent. 
• Month 2: 420%, still good. 
• Month 3: 380%, concerning. 
• Month 4: 310%, alarm bells.

What happened? 

The algorithm exhausted the most efficient audience segments and search terms. 

To keep growing volume – because it is designed to maximize – it expanded into less qualified traffic. 

Broad match reached further. Audiences widened. Bid efficiency declined.

Traffic quality deterioration

Sometimes the numbers look fine, but qualitative signals tell a different story. 

• Engagement declines – bounce rate rises, time on site falls, pages per session drop. 
• Geographic shifts appear as the algorithm drives traffic from lower-value regions. 
• Device mix changes, often skewing toward mobile because CPCs are cheaper, even when desktop converts better. 
• Time-of-day misalignment can also emerge, with traffic arriving when sales teams are unavailable.

These quality signals do not directly influence optimization because they are not part of the conversion data. 

To address them, the algorithm needs constraints: bid adjustments, audience exclusions, or ad scheduling.

The search terms report reveals the truth

The search terms report is the truth serum for AI bidding performance. 

Export it regularly and look for:

• Low-intent queries receiving aggressive bids.
• Informational searches mixed with transactional ones.
• Irrelevant expansions where the algorithm chased conversions into entirely different intent.

A high-end furniture retailer should not spend $8 per click on “free furniture donation pickup.” 

A B2B software company targeting “project management software” should not appear for “project manager jobs.” 

These situations occur when the algorithm operates without constraints. 

Keyword matching is also looser than it was in the past, which means even small gaps can allow the system to bid on queries you never intended to target.

Dig deeper: How to tell if Google Ads automation helps or hurts your campaigns

---

Strategic intervention points: When and how to take control

Segmentation for better control

One-size-fits-all AI bidding breaks down when a business has diverse economics. 

The solution is segmentation, so each algorithm optimizes toward a clear, coherent goal.

Separate high-margin products – 40%+ margin – into one campaign with more aggressive ROAS targets, and low-margin products – 10% to 15% margin – into another with more conservative targets. 

If the Northeast region delivers 450% ROAS while the Southeast delivers 250%, separate them. 

Brand campaigns operate under fundamentally different economics than nonbrand campaigns, so optimizing both with the same algorithm and target rarely makes sense.

Segmentation gives each algorithm a clear mission. Better focus leads to better results.

Bid strategy layering

Pure automation is not always the answer. 

In many cases, hybrid approaches deliver better results.

• Run Target ROAS at 400% under normal conditions, then manually lower it to 300% during peak season to capture more volume when demand is high. 
• Use Maximize Conversion Value with a bid cap if unit economics cannot support bids above $12. 
• Group related campaigns under a portfolio Target ROAS strategy so the algorithm can optimize across them. 
• For campaigns with limited conversion data or volatile performance, Enhanced CPC offers algorithmic assistance without full black box automation.

The hybrid approach

The most effective setups combine AI bidding with manual control campaigns.

Allocate 70% of the budget to AI bidding campaigns, such as Target ROAS or Maximize Conversion Value, and 30% to Enhanced CPC or manual CPC campaigns. 

Manual campaigns act as a baseline. If AI underperforms manual by more than 20% after 90 days, the algorithm is not working for the business.

Use tightly controlled manual campaigns to capture the most valuable traffic – brand terms and high-intent keywords – while AI campaigns handle broader prospecting and discovery. 

This approach protects the core business while still exploring growth opportunities.

COGS and cart data reporting (plus profit optimization beta)

Google now allows advertisers to report cost of goods sold, or COGS, and detailed cart data alongside conversions. 

This is not about bidding yet, but seeing true profitability inside Google Ads reporting.

Most accounts optimize for revenue, or ROAS, not profit. 

A $100 sale with $80 in COGS is very different from a $100 sale with $20 in COGS, but standard reporting treats them the same. 

With COGS reporting in place, actual profit becomes visible, dramatically improving the quality of performance analysis.

To set it up, conversions must include cart-level parameters added to existing tracking. 

These typically include item ID, item name, quantity, price, and, critically, the cost_of_goods_sold parameter for each product.

Google is testing a bid strategy that optimizes for profit instead of revenue. 

Access is limited, but advertisers with clean COGS data flowing into Google Ads can request entry. 

In this model, bids are optimized around actual profit margins rather than raw conversion value. 

This is especially powerful for retailers with wide margin variation across products.

For advertisers without access to the beta, a custom margin-tracking pixel can be implemented manually. It is more technical to set up, but it achieves the same outcome.

Dig deeper: Margin-based tracking: 3 advanced strategies for Google Shopping profitability

When AI bidding actually works

AI bidding works best when the fundamentals are in place: 

• Sufficient conversion volume.
• A stable business model with consistent margins and predictable seasonality.
• Clean conversion tracking.
• Enough historical data to support learning.

In these conditions, AI bidding often outperforms manual management by processing more signals and making more granular optimizations than humans can execute at scale.

This tends to be true in:

• Mature ecommerce accounts.
• Lead generation programs with consistent lead values.
• SaaS models with predictable trial-to-paid conversion paths.

When those conditions hold, the role shifts.

Bid management gives way to strategic oversight – monitoring trends, identifying expansion opportunities, and testing new structures.

The algorithm then handles tactical optimization.

Preparing for AI-first advertising

Google is steadily reducing advertiser control under the banner of automation. 

• Performance Max has absorbed Smart Shopping and Local campaigns. 
• Asset groups replace ad groups. 
• Broad match becomes mandatory in more contexts. 
• Negative keywords increasingly function as suggestions the system may or may not honor.

For advertisers with complex business models or specific strategic goals, this loss of granularity creates tension. 

You are often asked to trust the algorithm even when business context suggests a different decision.

That shift changes the role. You are no longer a bid manager. 

You are an AI strategy director who:

• Defines objectives.
• Provides business context.
• Sets constraints.
• Monitors outcomes.
• Intervenes when the system drifts away from strategic intent.

No matter how advanced AI bidding becomes, certain decisions still require human judgment. 

Strategic positioning – which markets to enter and which product lines to emphasize – cannot be automated. 

Neither can creative testing, competitive intelligence, or operational realities like inventory constraints, margin requirements, and broader business priorities.

This is not a story of humans versus AI. It is humans directing AI.

Dig deeper: 4 times PPC automation still needs a human touch

Master the algorithm, don’t serve it

AI-powered bidding is the most powerful optimization tool paid media has ever had. 

When conditions are right – sufficient data, a stable business model, and clean tracking – it delivers results manual management cannot match.

But it is not magic.

The algorithm optimizes for mathematical targets within the data you provide. 

If business context is missing from that data, optimization can be technically correct and strategically wrong. 

If markets change faster than the system adapts, performance erodes. 

If your goals diverge from Google’s revenue incentives, the algorithm will pull in directions that do not serve the business.

The job in 2026 is not to blindly trust automation or stubbornly resist it. 

It is to master the algorithm – knowing when to let it run, when to guide it with constraints, and when to override it entirely.

The strongest PPC leaders are AI directors. They do not manage bids. They manage the system that manages bids.

Shopify powers more than 6 million live ecommerce websites, supported by a robust app ecosystem that can extend nearly every part of the customer journey. 

Anyone can develop an app to perform virtually any function. 

But with so many integrations to choose from, ecommerce teams often waste time testing add-ons that promise revenue gains but fail to deliver.

Having worked across a wide range of Shopify implementations, I’ve seen which tools consistently improve checkout completion, recover abandoned carts, and increase revenue. 

Based on that experience, I’ve organized the most effective integrations into three tiers by priority – so you can implement the essentials first, then move on to more advanced optimization.

Tier 1: Mobile-first, frictionless buying

With 54.5% of holiday purchases happening on mobile, the ecommerce experience must be seamless and flexible. 

As a result, every Shopify site should have two components integrated into its storefront: 

• A digital wallet compatibility.
• A buy now, pay later (BNPL) option. 

Without these in place, Shopify users introduce unnecessary friction into the purchase journey and risk sending customers to competitors. 

The good news is that both components integrate natively with Shopify, requiring no custom development.

Why you need digital wallets

Digital wallets, such as Apple Pay, Google Pay, and PayPal, autofill delivery and payment information with a single click, eliminating the friction of typing on a small screen. 

This ease of use can shorten the purchase journey to just a few clicks between a social ad and checkout.

Adoption is accelerating. Up to 64% of Americans use digital wallets at least as often as traditional payment methods, and 54% use them more often.

Eliminate price objections with BNPL

Beyond payment convenience, customers also expect flexibility. 

BNPL providers, including Klarna and Afterpay, allow buyers to spread payments over time, reducing price objections at checkout. 

These options contributed $18.2 billion to online spending during last year’s holiday season – an all-time high, according to Adobe.

Together, digital wallets and BNPL form the foundation of a modern, mobile-first checkout experience. 

With these essentials in place, Shopify users can focus on tools that re-engage customers and bring them back to complete their purchases.

Dig deeper: The ultimate Shopify SEO and AI readiness playbook

Tier 2: The re-engagement power players

The second tier focuses on re-engagement – tools designed to bring back customers who have already shown intent. 

These integrations improve abandoned-cart recovery, increase repeat purchases, and build trust through social proof.

Re-engage customers with email and SMS

Email remains one of the most effective channels for re-engaging customers at every stage of the journey. 

Klaviyo and Attentive are strong options for Shopify users because both offer deep platform integration with minimal setup.

Both platforms also support SMS, allowing Shopify sellers to send automated text messages directly to customers’ mobile devices. 

SMS consistently delivers higher open, click-through, and conversion rates than email, making it especially effective for re-engagement use cases such as abandoned-cart recovery.

Together, these tools enable targeted campaigns and sophisticated automated flows that drive incremental revenue. 

However, CAN-SPAM and TCPA regulations require explicit opt-in for email and SMS marketing, respectively. 

As a result, sellers can only use these channels to contact customers who have agreed to receive marketing messages.

Use human-centered SMS outreach

While Attentive and Klaviyo effectively reach customers who have opted in to marketing, CartConvert helps sellers engage the 50% to 60% of shoppers who have not. 

The platform uses real people to contact cart abandoners via SMS. Because the outreach is not automated, TCPA restrictions do not apply.

CartConvert agents have live conversations with potential customers about their shopping experience. 

They are familiar with the products and can guide buyers back toward a purchase by suggesting alternatives or offering discounts. 

Running CartConvert alongside Klaviyo or Attentive ensures both subscribers and non-subscribers are included in re-engagement efforts.

---

Demonstrate social proof through reviews

Human-centered marketing also plays a role in building buyer confidence. 

Today’s online shoppers rely heavily on reviews when making purchasing decisions. 

When reviews are integrated directly into the shopping experience, they help establish trust and legitimacy, which in turn drive higher conversion rates. 

A product with five reviews is 270% more likely to be purchased than one with no reviews, research from the Spiegel Research Center at Northwestern University found.

Shopify users can choose from several review aggregators that pull Google reviews into product pages. 

Sellers should prioritize aggregators that also sync with Google Merchant Center, which powers Google Ads. 

Tools such as Okendo, Yotpo, and Shopper Approved integrate smoothly with both Shopify and Google’s ecosystem.

When reviews sync with Merchant Center, they can appear in Google Shopping ads, improving ad performance. 

While these tools add cost, they are also proven to generate incremental revenue that offsets the investment.

Dig deeper: How to make ecommerce product pages work in an AI-first world

Tier 3: Advanced optimization

The final tier includes more advanced integrations designed to help sellers optimize their sales funnel and performance at scale.

Attribution and analytics: Triple Whale

GA4’s changes to reporting, session logic, and interface have made attribution more difficult for many ecommerce teams. 

As a result, sellers are increasingly seeking clearer, independent performance insights.

Since 2023, Triple Whale has emerged as a leading alternative to Google Analytics, offering third-party attribution tools that integrate seamlessly with Shopify. 

The platform supports multiple attribution models – including first-click, last-click, and linear – along with cross-platform cost integration.

It also provides real-time data, which Google Analytics does not. 

This capability becomes especially valuable during high-pressure sales periods, such as Black Friday, when delayed reporting can lead to missed opportunities.

Although Triple Whale can cost up to $10,000 annually for mid-size brands, the improved data quality often justifies the investment for teams scaling paid acquisition.

Landing page customization: Replo

For sellers focused on improving conversion rates, landing page testing is essential. 

While Shopify is relatively easy to use, making changes to a live storefront for A/B testing carries the risk of breaking the site.

Replo allows Shopify users to build custom landing pages that can be tested at scale without coding. 

These pages typically provide a better user experience than default Shopify themes. 

It can also use site data to personalize landing pages based on a shopper’s browsing history. 

As a result, Replo-built pages often convert at higher rates than static site pages.

TikTok ads integration

TikTok continues to grow as a paid media channel, but it has traditionally presented a higher barrier to entry for advertisers. 

Previously, sellers needed an active TikTok account and could only purchase ads within the app, adding complexity and cost.

TikTok’s Shopify integration allows sellers to create ads that link directly to their websites, rather than keeping users inside the app. 

This change has lowered the barrier to entry and expanded access to the platform. 

Early testing shows promise for use cases such as cart abandonment, making the integration worth exploring despite its relative immaturity.

Dig deeper: Ecommerce SEO: Start where shoppers search

Prioritizing Shopify integrations for maximum impact

Shopify is a powerful platform for ecommerce, but maximizing results requires going beyond its default features. 

• Start with essentials such as digital wallets and BNPL to reduce checkout friction. 
• Then layer in email, SMS, and review integrations to re-engage interested shoppers. 
• Finally, add analytics, attribution, and landing-page testing to optimize performance at scale.

Sellers do not need to implement every solution at once. 

Instead, conduct a quick audit of the existing stack against this framework, identify gaps, and prioritize the tools that improve conversion and re-engagement. 

Shopify’s flexibility is its greatest strength, and its app ecosystem enables sellers to turn more visitors into buyers.

Optimizing for AI search is “the same” as optimizing for traditional search, Google SVP of Knowledge and Information Nick Fox said in a recent podcast. His advice was simple: build great sites with great content for your users.

More details. Fox made the point on the AI Inside podcast, during an interview with Jason Howell and Jeff Jarvis. Here is the transcript from the 22 minute mark:

Jarvis: “Is there guidance for enlightened publishers who want to be part of AI about how they should view, should they view their content in any way differently now?”

Fox: “The short answer is no. The short answer is what you would have built and the way to optimize to do well in Google’s AI experiences is very similar, I would say the same, as how to perform well in traditional search. And it really does come down to build a great site, build great content. The way we put it is: build for users. Build what you would want to read, what you would want to access.”

• This jives with what Danny Sullivan from Google said, that good GEO is good SEO.
• This echoes Google’s Gary Illyes advice from July – that all you need to do is normal SEO.

Why we care. Many of you have been practicing SEO for many years, and now with this AI revolution in Search, you should know you are very well equipped to perform well in AI Search with many, if not all, of the skills you learned doing SEO. So have at it.

The video. Is AI Search Hurting The Open Web? With Google’s Nick Fox // AI Inside #104

💾

We celebrated a major milestone in June: the return of SMX Advanced as an in-person event. It was our first since 2019.

More than a conference, SMX Advanced 2025 was a reunion. Search marketers from around the world came together to connect, exchange ideas, and learn the most current and advanced insights in search.

But search never stands still. With rapid shifts in AI SEO, constant algorithm changes, and the challenge of balancing generative AI with a human touch, the need for truly advanced, actionable education has never been greater.

Help shape SMX Advanced 2026

We’re committed to making the SMX Advanced 2026 program our most relevant, advanced, and exciting deep-dive experience yet. And we can’t do it without you – the expert community that makes this event legendary.

We’re inviting you to directly shape the curriculum for 2026.

Help us build a program that tackles the biggest challenges and opportunities on your radar by completing our short survey. Tell us:

• What advanced topics are most critical to your professional growth right now.
• Which recent search changes or complexities are keeping you up at night.
• Which search industry experts and innovators you need to hear from.
• Which session formats – from deep-dive clinics to lightning talks and interactive panels – will help you learn more and retain what you learn.

Fill out the survey here.

Be entered to win an All Access pass

To thank you for your time and insights, everyone who completes the survey will have the opportunity to enter an exclusive drawing.

One lucky participant will win a coveted All Access pass to SMX Advanced 2026, taking place June 3-5 at the Westin Boston Seaport.

Submit a session pitch

Beyond shaping the agenda, we also invite you to submit a session pitch. If you have a breakthrough strategy, an innovative case study, or next-level insights, this is your chance to help lead the industry conversation.

Read our guide to speaking at SMX for more details on how to submit a session idea. When you’re ready, create your profile and send us your session pitch.

We look forward to your submissions and insights! If you have any questions, feel free to reach out to me at kathy.bushman@semrush.com.

Google Search Console appears to have fixed the weeks-long delay in Performance reports. After several weeks of 50+ hour lag times, the reports now seem up to date as of the past few hours.

Now up-to-date. If you check the Search Performance report now, you should see a normal delay of about two to six hours. Over the past few weeks, that delay had stretched to more than 70 hours.

This is what I see:

The delays began a few weeks ago and took roughly three weeks to fully clear, including the backlog of data.

Page indexing report. Meanwhile, the Page Indexing report delay we reported weeks ago is still unresolved. The report is now almost a month behind, and Google has not fixed it yet. Google posted a notice at the top of the report that says:

• “Due to internal issues, this report has not been updated to reflect recent data”

Why we care. If you rely on Search Console data for analytics and stakeholder or client reporting, this has been extremely frustrating. The Performance reports now appear to be updating normally, but the Page Indexing report remains heavily delayed and will continue to create reporting headaches.

Meanwhile, Google released a number of new features in the past few weeks, including:

• AI-powered configuration for the Search Performance report
• Social channels in the Insights report
• Weekly and monthly smoothing in the Performance report

Managing large catalogs in Google Performance Max can feel like handing the algorithm your wallet and hoping for the best. 

La Maison Simons faced that exact challenge: too many products and not enough control. Then they rebuilt their segmentation with Channable Insights and turned a “black box” campaign into a revenue-generating machine.

Step 1: Stop segmenting by category

Simons originally split campaigns by product category. It sounded logical – until their best-selling sweater ate the budget and newer or overlooked products never had a chance to surface.

Static segmentation meant limited visibility and slow decisions.

Marketers stayed stuck making manual tweaks while Google kept auto-prioritizing only what was already working.

Step 2: Segment by performance

Enter Channable Insights. Product-level performance data (ROAS, clicks, visibility) now powers dynamic grouping:

Products automatically move between these segments as performance shifts – no manual work needed. As Etienne Jacques, Digital Campaign Manager, Simons, put it:

“One super popular item no longer takes all the money.”

Step 3: Shorten your analysis window

Instead of waiting 30 days for signals, Simons switched to a rolling 14-day window.

The result: faster reactions, sharper accuracy, and less wasted spend in a fast-moving catalog.

Step 4: Push the strategy across channels

Why stop at Google? The same segmentation logic was automatically applied on:

• Meta
• Pinterest
• TikTok
• Criteo

Cross-channel consistency creates compounding optimization.

Step 5: Watch the metrics climb

Without raising ad spend, Simons unlocked:

• ROAS growth: from ~800% to ~1500%
• CPC decrease: $0.37 to $0.30
• CTR lift: 1.45% to 1.86%
• 14% increase in average order value
• 1300% ROAS for New Arrivals campaigns
• Faster workflows and fewer manual tweaks

Even the “invisibles” turned into surprise profit drivers once they finally got the spotlight.

Step 6: Treat automation as control, not chaos

Automation restored marketing control – it didn’t remove it.

Teams can finally learn from the data and influence which products grow, instead of letting PMax run everything on autopilot.

Your action plan

• Classify products as Stars, Zombies, and New Arrivals.
• Automate campaign reassignment based on real-time data.
• Refresh product insights every 14 days.
• Roll out segmentation logic to every paid channel.
• Scale what wins – test what hasn’t yet.

Want Simons-style ROAS gains without extra ad spend? Start by testing the quality of your product data with a free feed and segmentation audit.

Google Ads launched VTC-optimized bidding for Android app campaigns, letting advertisers toggle bidding toward conversions that happen after an ad is viewed rather than clicked.

Previously, VTC worked as a hidden signal inside Google’s systems. Now, it’s a clear, explicit optimization option.

The shift. Google is shifting app advertising away from click-centric logic and toward incrementality and influence, especially for formats like YouTube and in-feed video. This update aligns bidding more closely with how users actually discover and install apps.

Why we care. You can now bid beyond clicks, improving measurement for video-led app campaigns and strengthening the case for upper-funnel activity.

Who benefits most. Video-first app advertisers and teams focused on awareness, engagement, and long-term growth – not just last-click installs.

What to watch

• Increased reliance on Google’s attribution model.
• Potential changes in CPA expectations.
• Greater emphasis on creative quality over click-driving tactics.

First seen. This update was first spotted by Senior Performance Marketing Executive Rakshit Shetty when he posted on LinkedIn.

Sergey Brin, Google’s co-founder, admitted that Google “for sure messed up” by underinvesting in AI and failing to seriously pursue the opportunity after releasing the research that led to today’s generative AI era.

Google was scared. Google didn’t take it seriously enough and failed to scale fast enough after the Transformer paper, Brin said. Also:

• Google was “too scared to bring it to people” because chatbots can “say dumb things.”
• “OpenAI ran with it,” which was “a super smart insight.”

The full quote. Brin said:

• “I guess I would say in some ways we for sure messed up in that we underinvested and sort of didn’t take it as seriously as we should have, say eight years ago when we published the transformer paper. We actually didn’t take it all that seriously and didn’t necessarily invest in scaling the compute. And also we were too scared to bring it to people because chatbots say dumb things. And you know, OpenAI ran with it, which good for them. It was a super smart insight and it was also our people like Ilya [Sutskever] who went there to do that. But I do think we still have benefited from that long history.”

Yes, but. Google still benefits from years of AI research and control over much of the technology that powers it, Brin said. That includes deep learning algorithms, years of neural network research and development, data-center capacity, and semiconductors.

Why we care. Brin’s comments help explain why Google’s AI-driven search changes have felt abrupt and inconsistent. After years of hesitation about shipping imperfect AI, Google is now moving fast (perhaps too fast?). The volatility we see in Google Search is collateral damage from that catch-up mode.

Where is AI going? Brin framed today’s AI race as hyper-competitive and fast-moving: “If you skip AI news for a month, you’re way behind.” When asked where AI is going, he said:

• “I think we just don’t know. Is there a ceiling to intelligence? I guess in addition to the question that you raised, can it do anything a person can do? There’s the question, what things can it do that a person cannot do? That’s sort of a super intelligence question. And I think that’s just not known, how smart can a thing be?”

One more thing. Brin said he often uses Gemini Live in the car for back-and-forth conversations. The public version runs on an “ancient model,” Brin said, adding that a “way better version” is coming in a few weeks.

The video. Brin’s remarks came at a Stanford event marking the School of Engineering’s 100th anniversary. He discussed Google’s origins, its innovation culture, and the current AI landscape. Here’s the full video.

💾

Google has updated its JavaScript SEO basics documentation to clarify how Google’s crawler handles noindex tags in pages that use JavaScript. In short, if “you do want the page indexed, don’t use a noindex tag in the original page code,” Google wrote.

What is new. Google updated this section to read:

• “When Google encounters the noindex tag, it may skip rendering and JavaScript execution, which means using JavaScript to change or remove the robots meta tag from noindex may not work as expected. If you do want the page indexed, don’t use a noindex tag in the original page code.”

In the past, it read:

• “If Google encounters the noindex tag, it skips rendering and JavaScript execution. Because Google skips your JavaScript in this case, there is no chance to remove the tag from the page. Using JavaScript to change or remove the robots meta tag might not work as expected. Google skips rendering and JavaScript execution if the robots meta tag initially contains noindex. If there is a possibility that you do want the page indexed, don’t use a noindex tag in the original page code.”

Why the change. Google explained, “While Google may be able to render a page that uses JavaScript, the behavior of this is not well defined and might change. If there’s a possibility that you do want the page indexed, don’t use a noindex tag in the original page code.”

Why we care. It may be safer not to use JavaScript for important protocols and blocking of Googlebot or other crawlers. If you want to ensure a search engine does not rank a specific page, make sure not to use JavaScript to execute those directives.

The SEO industry is entering its most turbulent period yet.

Traffic is declining. AI is absorbing informational queries. 

Social platforms now function as search engines. Google is shifting from a gateway to an answer engine.

The result is a sector running in circles – unsure what to measure, what to optimize, or even what SEO is meant to do.

Yet within this turbulence, something clear has emerged.

A single marketing metric that cuts through the noise and signals brand health and future demand. 

A metric that marketers and SEOs can align around with confidence.

That metric is share of search.

Discovery is changing, and measurement must change with it

The old model of being discovered by accident through classic search behavior is disappearing.

AI Overviews answer questions without sending traffic anywhere. 

Meta is already rolling out its own AI to answer user queries. 

TikTok and YouTube continue to grow as product discovery engines. 

It is only a matter of time before LinkedIn becomes a business search engine powered by conversational AI.

We are witnessing a seismic shift. In moments like this, measurement becomes even more important. 

Many SEO metrics are losing meaning, but one is rapidly gaining importance.

What share of search actually measures

Share of search is a metric developed by James Hankins and Les Binet. 

It is calculated by dividing a brand’s search volume by the total search volume for all brands in its category. 

The result shows the proportion of category interest the brand commands.

The value is not in the calculation itself, but in what the metric correlates with.

Studies published by the Institute of Practitioners in Advertising (IPA) show that share of search correlates strongly with market share and future buying behavior. 

As the IPA notes:

• “Share of search is a leading indicator or predictor of share of market. When share of search goes up, share of market tends to rise. When share of search goes down, share of market falls.”

In simple terms, consumers search for brands they are considering, buying, or using. 

That makes search behavior one of the clearest available signals of real demand.

Share of search was never designed to be perfect. It does not capture every nuance of how people find information across platforms. 

It was built as a practical proxy for brand demand – and right now, practical measurement is exactly what the industry needs.

Dig deeper: Measuring what matters in a post-SEO world

From traffic to demand: Why marketers need a new signal

Traffic as a measurement has become almost meaningless. 

It has been easy to inflate, manipulate, and misunderstand.

Goodhart’s Law explains why. When a measure becomes a target, it stops being a good measure. 

Traffic was treated as a target for years, and as a result, it stopped being a reliable indicator of anything meaningful.

Now traffic is falling – not because brands are doing anything wrong, but because AI is answering questions before users ever reach a website.

Ironically, this makes traffic more meaningful again, as much of the noise that once inflated it is disappearing.

The bigger advantage, however, belongs to share of search. 

It cannot be inflated through content tactics or gamed by chasing trends. It reflects underlying consumer interest.

That is why share of search has become so significant. 

It shows whether a brand is being searched for more or less than its competitors. 

When share of search rises, brand demand is growing. When it falls, demand is weakening.

If an entire category collapses – as it did with air fryers once most consumers had already bought one – the metric also provides a clear signal that demand for the overall market is shrinking.

There is another advantage. Share of search is a multi-platform metric.

A metric that crosses platforms

People no longer search in one place. 

Product searches may begin on Amazon, TikTok, or Facebook. 

Credibility checks often happen on YouTube. Long-form research may still take place on Google.

Discovery is fragmented, and behavior is fluid.

Share of search adapts to this reality. It is platform agnostic. 

You can measure it using Google Trends, Ahrefs, Semrush, My Telescope, or any platform that provides reliable volume estimates. 

You can track demand across Amazon, TikTok, YouTube, and emerging AI search interfaces.

Where the behavior happens matters less than the signal itself. 

If people are looking for your brand, they are demonstrating intent.

This cross-platform visibility is critical because AI search sends little traffic to websites. 

ChatGPT, Claude, and other LLMs present answers, snippets, and summaries, but rarely generate click-through. 

Links are often buried, inaccessible, or accompanied by friction.

Instead, these systems trigger brand search. 

Users encounter a brand in an AI response, then search for it when they want more information.

As a result, share of search becomes the tail-end signal of everything marketing does, including AI exposure. 

When share of search rises, marketing is working. When it falls, it is not.

However, the metric needs a champion.

---

A metric SEOs should champion

The SEO industry has spent years focused on two types of keywords: 

• Non-brand buyer intent.
• Non-brand informational. 

That approach made sense when classic search was the dominant discovery channel. That world is disappearing.

Yet many SEOs continue to cling to outdated deliverables, such as structured data micro-optimization or churning out endless blog posts to influence hypothetical AI citations.

Citations are a distraction. 

At best, they are a minor signal in LLM outputs. 

At worst, they are a misleading metric that will not stand up to financial scrutiny. 

When CFOs start questioning the value of SEO budgets, citations will not hold up as evidence of ROI.

Share of search will.

SEOs who embrace share of search position themselves not as keyword tacticians, but as strategic insights partners. 

They become interpreters of demand who help:

• CMOs understand whether brand marketing is breaking through.
• Leadership teams see where consumer interest is rising or falling.

This shift changes the role of SEO entirely. 

Instead of being judged by how much content they produce, SEOs begin to be valued for how well they understand search behavior and the commercial impact of that behavior.

A well-structured share of search report tells a coherent story:

• Is the brand being searched for more this quarter?
• Are competitors gaining ground?
• Is the category contracting?
• Did a recent PR campaign increase branded search?
• Did a product launch move the needle?

In the AI era, this narrative becomes essential. 

Someone inside the organization must understand how people search, where they search, and what the numbers mean.

SEOs are naturally positioned to fill that role. You have the background and the expertise. 

And as AI automates more mechanical SEO tasks, this progression becomes increasingly natural.

Because share of search requires interpretation.

Dig deeper: Why LLM perception drift will be 2026’s key SEO metric

The depth and complexity available

Share of search does not have to be a single top-level number. It can be:

• Broken down by product line, model, or competitive set. 
• Segmented into branded and semi-branded queries.
• Tracked across every channel where search behavior exists.
• Compared against AI model outputs to understand where visibility aligns or diverges.

Consider the air fryer category. 

Demand collapsed across the market once most consumers had already purchased one. 

Within that collapse, however, individual models rose and fell based on their appeal. 

Ninja’s latest model, for example, showed spikes and dips that revealed shifts in consumer interest long before sales data arrived.

Share of search acts as early detection for market movement.

SEOs who understand this level of nuance become indispensable. They can:

• Advise whether a category is shrinking or whether a competitor is accelerating. 
• Identify gaps in PR coverage.
• Highlight where LLMs reference competitor brands more frequently.
• Signal when product positioning needs reinforcement.

This is the future skill set – not chasing rankings, but interpreting behavior.

A human role that AI can’t replace

As AI becomes more integrated into search and site optimization, many mechanical SEO tasks will be increasingly automated. 

The interpretation of marketing performance, however, cannot be fully automated.

Share of search requires human judgment. 

It requires an understanding of context, seasonality, category dynamics, and brand strategy. 

That role can and should belong to the SEO professional.

Some agencies may label this function an insights specialist or a data analyst. 

Some organizations may house it within marketing. 

But the people who understand search behavior most deeply are SEOs. 

They are best positioned to interpret what the numbers mean and communicate those insights to leadership teams.

Leadership teams need to understand what is happening with their brand.

The metric that protects brands in the AI era

Marketing leaders are already discussing share of search, and it is beginning to appear in boardroom conversations. 

It is quickly becoming a central indicator of brand strength. 

In an AI-driven world where traffic is scarce and visibility is fragmented, the strategic imperative is clear.

Brands need to be searched for. Those that are searched for endure. Those that are not fade.

That is why share of search is not just another metric. It is becoming the metric. 

SEOs who embrace it can elevate their role, influence, and strategic value at exactly the moment the industry needs it most.

Your next steps 

The advice for SEOs is simple: Learn share of search.

To get started:

• Learn more about the metric by reading reports and studies.
• Create your first share of search report.
• Analyze the drivers of change, such as market shifts or recent PR or TV campaigns.
• Experiment with search tools to determine which reporting approach works best.
• Involve other departments. Host a session on share of search and collaborate with PR teams to track activity.

You will not become fluent in the metric without using it. Once you do, its applications become clear.

Share of search is the bridge that connects SEO to the broader world of brand.

Take the first step.

As marketing channels and touchpoints multiply rapidly, the way success is measured significantly impacts long-term growth and executive perception. 

Click-based attribution – across models like last-click, first-click, linear, and time-decay – remains the default. 

But as a standalone measurement strategy, it’s showing its age. 

Click metrics now carry disproportionate weight in executive dashboards, and that reliance introduces real limitations.

Click-based models can still reveal valuable insights into digital engagement. 

However, when the C-suite bases major budget and strategy decisions solely on clicks, they risk overlooking critical aspects of the customer journey – often the very pieces that matter most.

This article examines:

• What click-based attribution actually captures.
• Where click-based measurement breaks down in a multi-channel, multi-device, privacy-first world.
• The business risks of over-indexing on click metrics.
• Measurement approaches that better align marketing with real business outcomes.
• How marketing leaders can guide executives toward more holistic, outcome-oriented frameworks.

The goal isn’t to demonize clicks – they still belong in the toolbox. But they should provide context, not serve as the foundation.

What does click-based attribution actually measure?

Click-based attribution tracks ad clicks and assigns conversion credit to the marketing touchpoints that drove them. 

Models like first-click, last-click, linear, time-decay, and data-driven approaches differ only in how they split that credit across the user journey.

Digital ad platforms and many analytics tools default to click-based models because clicks are relatively easy to capture, understand, and report. 

They’re deterministic, clean, and simple to interpret at a glance.

That cleanliness, however, can be misleading. 

Click-based attribution depends entirely on a user interacting with tracking links or tags. 

If a user doesn’t click, or clicks but converts later or elsewhere, the touchpoint may be missed or misattributed.

This approach can work in a simple, linear funnel. 

But as customer journeys become multi-device, multi-channel, and increasingly offline, clicks lose context quickly.

Dig deeper: The end of easy PPC attribution – and what to do next

The problems with solely relying on click-based attribution

Clicks don’t represent real customer behavior

Today’s buyers rarely follow the neat, linear paths that click-based models assume. 

Instead, they move across devices, channels, and even offline touchpoints.

Think social media, LLMs like ChatGPT, and brand exposure from video, influencers, or website content. 

Many of these interactions never generate a tracked click, yet they play a critical role in shaping perception, intent, and eventual conversion.

For example, a buyer may watch a brand’s video on LinkedIn during their morning commute. 

Later, they read a third-party review and skim a few case studies on the brand’s website.

Days later, they type the brand name directly into Google and convert. 

In a click-based model, only the final branded search click receives credit. 

The video, the review, and the content that built trust remain invisible.

These aren’t minor attribution blind spots – they represent a canyon. 

Click-based measurement skews too much toward lower-funnel performance

Click-based models place the most weight on the final click. 

As a result, they often over-index lower-funnel activity from channels like retargeting ads or branded search. 

These channels convert more frequently, but they do not create demand on their own.

For C-level decision-makers, this creates a dangerous bias. 

Dashboards light up for retargeting campaigns and branded search, so budgets flow there.

Mid- and upper-funnel investments – brand building, awareness, content, and influencers – are reduced or cut. 

Over time, the brand’s long-term growth engine is choked in favor of short-term, easily quantifiable wins.

Dig deeper: Marketing attribution models: The pros and cons

Click-based models undervalue creative, messaging, and brand

Not all marketing impact shows up as clicks. 

A video ad or thought-leadership piece may plant a seed without prompting an immediate click, yet the message can linger. 

It may lead to later brand searches or site visits, outcomes that are difficult to capture through click-based measurement.

As a result, brand power, creative messaging, and top-of-funnel reach are underrepresented in click-based models. 

Over time, organizations that optimize solely around click-based attribution may unintentionally deprioritize creativity, brand-building, and long-term equity.

Click-based attribution breaks down in a privacy-first world

We’re moving toward a future where third-party cookies are diminished or gone, privacy rules continue to tighten, and tracking becomes less precise. 

Under these conditions, click tracking grows more difficult, less reliable, and increasingly misaligned.

Without stable identifiers, many of the assumptions behind click-based models – “this click belongs to that user” or “this click led to that conversion” – begin to unravel. 

Attribution becomes a house of cards built on data that may not hold up as privacy and tracking norms continue to shift.

The business risks of over-relying on click-based attribution

Misallocation of budgets

When click-based reporting dominates, budgets tend to flow toward what looks good – the activities that drive visible revenue and deliver clean, direct ROI. 

That often comes at the expense of demand generation efforts that support long-term growth, such as brand campaigns, content, awareness, and other upper-funnel media.

This approach may “work” for a few months or even years. 

Over time, however, the pipeline dries up. 

Awareness declines, organic reach stagnates, and the brand loses its ability to attract new audiences at scale.

Erosion of brand over time

Marketing shifts into a zero-sum exercise focused on extracting conversions from existing demand rather than expanding it. 

Without sustained investment in brand equity and demand generation, competitiveness, brand loyalty, and lifetime value (LTV) suffer.

In essence, optimizing for short-term ROAS puts long-term brand health at risk.

Misaligned incentives across teams

When KPIs are click-based:

• Media teams optimize for clicks.
• Creative teams optimize for click-worthy content.
• Analytics teams optimize for attribution that ties cleanly to conversions. 

The result is marketing silos working toward different objectives.

• Media buys may undermine creative performance. 
• Creative teams may chase cheap clicks. 
• Analytics may mask cannibalization rather than reveal incrementality. 

Fragmentation increases.

Blind trust in platform-reported metrics

Ad platforms and tracking tools report click-based conversions, but many of those conversions are self-crediting, particularly within paid media platforms. 

When you rely heavily on these numbers without scrutiny or connection to the broader user journey, you risk making high-stakes decisions based on biased data.

---

What to use instead of click-based attribution

If click-based attribution is flawed, how should performance be evaluated? 

The short answer is a combination of approaches grounded in real business outcomes.

Marketing mix modeling (MMM) for channel-level contribution

At a higher level – especially when multiple channels are involved, including online, offline, paid media, organic media, and PR – MMM helps quantify channel-level contribution to sales, revenue, or other business outcomes. 

It looks at broad correlations over time using aggregated data rather than user-level clicks.

MMM, supported by machine learning, improved data resolution, and more frequent refresh cycles, has become more accessible and actionable. 

It isn’t a replacement for click- or site-based data, but a powerful complement. 

Dig deeper: MTA vs. MMM: Which marketing attribution model is right for you?

Multi-touch attribution (MTA), used thoughtfully 

User-level path analysis still has a place when privacy and tracking allow. 

Multi-touch models that consider multiple touchpoints can provide richer insight, but they work best as one input among many rather than a single source of truth. 

They offer path visibility, but without incrementality testing or support from MMM, they still risk over-crediting and bias.

Customer lifecycle metrics: LTV and CAC payback, retention, cohort analysis

Marketing value isn’t confined to a single sale or conversion.

LTV, retention, and long-term value creation matter just as much. 

Tying spend to CAC payback, churn, loyalty, and retention creates a measurement framework aligned with long-term business goals.

Incrementality testing as a standard practice

Incrementality testing measures what marketing actually adds by identifying net-new conversions, revenue, lift, or awareness. 

It separates what would have happened anyway from what your efforts truly drove.

This approach isn’t as clean as click tracking and requires more planning and discipline, but it delivers causality. 

It allows you to say, with confidence, “This spend generated X% incremental lift.”

Dig deeper: Why incrementality is the only metric that proves marketing’s real impact

Attention metrics, quality signals, and creative impact

Not all impact is transactional. 

Upper-funnel signals such as viewability, time-in-view, attention scores, and engagement matter. 

Creative resonance, brand recall, and impact often influence later behavior that never appears as a click.

Looking beyond clicks to metrics like creative recall, brand lift, share of voice, sentiment, and qualitative feedback helps anchor measurement to real brand value and audience expectations.

Building a modern measurement framework

A modern measurement framework isn’t built around one model or metric. 

It brings together complementary methods to create a clearer, more balanced view of performance.

Take a portfolio approach

The most effective measurement frameworks take a portfolio approach. 

MMM, incrementality, multi-touch attribution (when possible), attention metrics, and customer lifecycle metrics work together to triangulate performance from multiple perspectives.

This diversity reduces bias and balances short-term performance with long-term brand health.

It also makes it possible for the C-suite to see more than conversions alone – including impact, growth potential, and sustainable value.

KPIs that reflect real business impact

Executives care about revenue, margin, and growth. Not just clicks. 

Reframe KPIs around the key metrics that matter, such as:

• Revenue.
• Cost per acquisition.
• Customer lifetime value.
• Retention.
• Brand lift.
• Market share.
• Brand sentiment.

Package those into dashboards that tell a story: 

• “Here’s what we did, here’s what grew, here’s what we learned, here’s where we go next.”

Build executive dashboards for outcomes, not vanity metrics

When dashboards lead with vanity metrics like click volume, CTR, or raw conversion rate, insight is limited. Lead instead with business outcomes.

Build narrative-driven dashboards that connect investment to results, learning, and action.

Lean toward data storytelling instead of data reporting. 

That story resonates with executives. It links marketing to business value, not just to marketing activity.

Leverage AI, predictive modeling, and forecasting strategically 

Modern analytics tools – including AI and predictive forecasting – can help:

• Estimate demand.
• Forecast impact.
• Model how different investments may play out over time. 

Use them to simulate scenarios, test assumptions, and support business cases.

These tools aren’t silver bullets. They work best as accelerators for sound strategic thinking. 

Moving away from click-based thinking

Changing how performance is measured doesn’t happen automatically.

It requires clear framing, evidence, and a deliberate transition rather than an abrupt overhaul.

Understand common objections and address them clearly

Often, executives cling to click-based metrics because they’re easy to understand (“one user clicked, we got a sale”) and seemingly real-time. 

They want fast feedback and accountability. Demand creation efforts often feel abstract and hard to justify.

Be prepared to address that directly:

• “Clicks are easy to understand.”
  • Yes. But they paint an incomplete picture. Show them what they miss.
• “We need real-time metrics to manage marketing spend.”
  • That’s valid. But real-time doesn’t always equal real value. Complement with more holistic time-based analyses based on the timing of your sales cycle, incremental lift tests, and periodic MMM to ground real-time decisions.
• “Brand/awareness spend is hard to justify.”
  • I hear you. That’s why you start small. Run test campaigns, measure impact via lift studies, attribution-aware conversion, and lifecycle metrics. Show proof-of-concept.

Implement a gradual shift, don’t overhaul overnight

Click-based attribution doesn’t need to be discarded overnight. Instead:

• Introduce incrementality testing for a small portion of spend to show what budget really contributes.
• Once incrementality proves meaningful lift, allocate more budget toward long-term demand creation efforts.
• Run or commission MMM annually (or semi-annually) to quantify channel contribution holistically.
• Adjust executive dashboards to reflect new KPIs, such as revenue, CAC payback, brand lift, and LTV, and reduce emphasis on mere clicks or last-click conversions.

Over time, incentives begin to shift. Media moves beyond clicks, creative focuses on quality and resonance, and analytics emphasizes causality and long-term value.

Educate the executive team

Executives rarely object to logic – they object to noise. 

Frame your case with clarity and use data. 

Show examples, run tests, show incremental lift, and then build dashboards that tell a clear story.

Once you prove that a dollar invested in brand or top-of-funnel media delivers compounding value over time, leadership hopefully becomes less attracted to short-term click metrics. 

They begin to appreciate marketing as an investment, not a cost center.

Clicks are part of the story, not the whole story

Click-based attribution has served marketing teams for years. It offered a clean way to connect conversions to touchpoints. 

But the landscape has changed. 

• User journeys are longer and messier. 
• Privacy constraints are tighter. 
• Long-term brand value now matters as much as short-term conversions.

For C-level teams, judging performance by clicks alone is like judging a company’s health by heart rate alone. It’s useful, but incomplete.

Modern marketing requires a richer view – one that blends data, causality, business outcomes, and long-term brand building.

As marketing leaders, our job isn’t to chase the next click. 

It’s to build brands that last, drive sustained growth, and help leadership see marketing not as a cost, but as a strategic investment.

Every week, new data highlights both the overlap and the divergence between effective organic search techniques across traditional SEO (Google SERPs) and GEO (ChatGPT, AI Overviews, Perplexity, etc.). 

It’s a lot to absorb. One week, headlines say traditional SEO tactics work fine for ChatGPT.

The next, you’ll see reports that one platform is elevating Reddit while another is dialing it back.

Given how quickly this landscape shifts, I want to break down the approach, process, and resources my team is using to tackle content in 2026. 

This goes far beyond a content calendar. 

It’s about combining audience understanding, the interplay of organic platforms, and your brand’s perspective to build a content system that delivers real value.

The right approach for valuable content

The emphasis on quality and value in content is good for marketers.

The tenets of E-E-A-T remain central to our approach because they apply to AI search discoverability as much as to traditional SEO. 

Producing strong content still depends on a rich understanding of your audience, good fundamental structures, and solid delivery methods – skills that always matter.

Start with your audience. 

• Who are they? 
• What do they need? 
• What content will help them get there? 

Approach content like any other product or service: 

• Identify a need and address it.
• Understand the emotions involved.
• Show your credentials – including third-party brand mentions, which are a leading factor in AI search visibility. 

Approach content like any other product or service:

• Find or understand a need and address it.
• Know the emotions (i.e., fear, uncertainty, urgency) in play.
• Show your credentials (in the form of authority, expressed in part by third-party brand mentions that are one of the leading factors of AI search visibility traction).

That said, content that has performed well in Google may not work as effectively for LLM search. 

Instead of writing primarily for blue-link SERPs, we now focus on creating content that stands on its own as an authoritative, structured data source, with trust and originality as ranking signals. 

That means prioritizing clarity, factual depth, and a consistent brand perspective that AI models can reliably quote.

In an age of mass AI content, original insights, data, and human perspective are key differentiators, so content systems should include a step for “original proof” – data, interviews, or commentary that make the material uniquely trustworthy.

We’re also thinking more about how content gets used in AI experiences, not just how it’s found. 

Summaries, bullet points, and explainers that answer layered intent are increasingly valuable. 

Incorporating schema, structured data, and a consistent brand voice improves how AI systems read and represent your content. 

In short, the goal is to optimize for retrievability and credibility, not just ranking.

---

Building a process to create valuable content

The content strategy path I like to prescribe is as follows:

• Problem aware: Empathize with your audience by articulating their problem in a clear, differentiated way.
• Solution aware: Present your audience with objective, detailed, valuable options for solutions to their problem.
• Brand aware: Develop your brand’s association as a trusted solution provider.
• Product aware: Position your specific product or service as the ideal solution for the reader’s problem.

Once your research is conducted, you’ll have what you need to craft content and deploy it in multiple ways. 

The linear workflow that persisted for years in traditional SEO, however, must evolve into a modular content engine – one where a single research output fuels multiple media types (articles, YouTube scripts, short-form video, LinkedIn posts, etc.), with platform-native variations all aligned to a central narrative theme.

Resources to use in content development

A few years ago, I would have started with well-known, well-established tools like Ahrefs and Semrush. 

While those remain useful for benchmarking, they no longer represent how people discover or consume information as AI search transforms user behavior in real time. 

AI search abstracts away keywords – users are asking multi-intent questions, and LLMs are generating synthesized answers. 

SEO analysis is now, rather than the main starting point, one piece of the research pie. 

It’s still important, but search optimization is now embedded throughout the content process.

The tools below have been important in the past, and my team still leans on them as part of a more holistic approach to content planning.

Qualitative interviews

Surveys are useful but can be expensive when you’re trying to reach audiences outside your CRM. 

You can still get strong insights by engaging subject matter experts who share the same professional experiences, challenges, and responsibilities as your target audience. 

Slack communities, live or virtual meet-ups, and memberships in organizations like the AMA or ANA can all offer on-the-ground perspectives that support your content mapping.

Audience analysis from AI systems 

It’s critical to include intent analysis from AI tools and conversational search data. 

Understanding how users phrase questions to AI systems can inform structure and tone.

Social media

Not all social media posts are created equal, but understanding your audience includes knowing where your audience likes to engage: X, Reddit, YouTube, TikTok, etc. (Not to mention that Reddit citations show up prominently in ChatGPT results.)

Utilize these platforms to gather real-time information on what your audience is discussing and to increase brand mentions, which will send strong signals to ChatGPT and similar tools.

Competitor analysis

Shift from tracking keyword overlap to evaluating content depth, originality, and entity coverage – where your brand’s expertise can fill gaps or improve on generic AI-summarized answers.

Adjust the KPIs to assess the impact of your content

For many years, SEO marketers focused on impressions and clicks, although more advanced practitioners also incorporated down-funnel metrics, such as leads, conversions, pipeline impact, and revenue. 

Today, SEOs must expand their KPIs to include brand mentions in:

• AI summaries.
• Content-assisted conversions.
• Cross-channel engagement depth. 

These are the new indicators of helpfulness and value.

Resist the urge to rest on your laurels

We’ve seen strong successes with AI search visibility that complement our traditional SEO results, but our understanding of best practices continues to evolve with each new round of aggregated data on AI search results and shifting user behavior.

In short, keep a parallel track of what has worked recently and where the trends are heading, since ChatGPT and its competitors are changing user behavior in real time – and with it, the shape of organic discovery across platforms.

This season, Google Search and Shopping Ads are expected to surge past $70 billion in holiday spending. But there’s a hidden flaw in the auction system — one most advertisers don’t realize is costing them money even when competitors aren’t in the game.

BrandPilot calls this the Uncontested Google Ads Problem, and it’s becoming one of the most overlooked sources of wasted ad spend in peak retail season.

During SMX Next, John Beresford, Chief Revenue Officer at BrandPilot, unpacked how a little-known behavioral quirk in Google’s auction logic can cause advertisers to overspend on their own brand terms, their Shopping placements, and even their category keywords — simply because Google doesn’t automatically reduce your CPC when competition disappears.

Instead of paying less when you’re the only bidder, you may be paying the same high rate you’d pay when rivals are active… without realizing it.

It’s a phenomenon happening thousands of times a day across major brands, and many marketers never notice it’s occurring.

In his session, Beresford discussed:

• Why “competition gaps” happen far more often than advertisers think.
• How uncontested moments distort CPCs, even on brand keywords.
• What real-time auction visibility makes possible — and why AI is changing the game.

He also shared examples of how advertisers are reclaiming wasted spend and reinvesting it into growth – without sacrificing impression share, traffic, or revenue.

Watch BrandPilot’s session now (for free, no registration required) to learn how to:

• Pinpoint why your CPCs are being artificially inflated when competitors are absent.
• Estimate the true financial impact of the Uncontested Ads Problem across your annual budget.
• Implement AI-driven bidding and suppression strategies that prevent self-bidding and boost ROAS.

If you’re running Google Search or Shopping campaigns this holiday season, you can’t afford to miss this session. Learn how to stop the Google Grinch from stealing your budget — and start turning those savings into real performance gains.

On episode 334 of PPC Live The Podcast, I speak to Sophie Fell Head of Paid Media at Liberty Marketing Group about a real PPC mistake involving location targeting. The conversation focuses on how small oversights can have big consequences—and how to recover from them professionally.

The PPC F-Up: worldwide location targeting

Sophie accidentally launched a campaign with worldwide location targeting enabled instead of restricting it to the client’s service area. In just a couple of days, the campaign generated around 1,500 leads that looked impressive on paper but were unusable because they came from outside the target locations.

When great results are a warning sign

The unusually strong performance initially looked like a win, but it became a red flag. When Sophie reviewed the campaign more closely, she discovered the location setting issue. This highlights an important PPC lesson: results that look too good should always be investigated, not celebrated blindly.

Handling the client conversation

The client spotted the issue around the same time Sophie did, while she was already preparing to flag it. The situation was handled with honesty—acknowledging the mistake, explaining what happened, and fixing it immediately. Transparency helped preserve trust, even though the client was understandably unhappy.

Why the mistake happened

This wasn’t a lack of knowledge—it came down to moving too quickly and relying on assumed checks rather than confirmed ones. Like many experienced practitioners, Sophie thought the setting had already been reviewed. The experience reinforced how dangerous platform defaults can be.

The long-term outcome

Once corrected, the campaign went on to perform exceptionally well. The client hit their targets six weeks early and exceeded revenue expectations by £3.5 million. The initial mistake didn’t define the outcome—how it was handled did.

What Sophie does differently now

Sophie now checks campaign settings multiple times, both before and after launch. She reviews settings whenever performance spikes or dips and never reports results without rechecking fundamentals. The key change is recognising that post-launch reviews often reveal what pre-launch checks miss.

Advice for when you’ve made a PPC mistake

Sophie’s guidance is simple: pause, investigate, and be honest. Check metrics and settings immediately, take responsibility, explain what went wrong, and clearly outline how you’ll prevent it from happening again. Mistakes become serious problems only when they’re mishandled.

Common PPC mistakes still seen today

Sophie regularly audits accounts that haven’t been updated for years, rely heavily on brand campaigns, or misuse automation like Performance Max. She also sees poor alignment between keywords, ads, and landing pages—fundamentals that still matter, even in AI-driven campaigns.

Why talking about mistakes matters

Many PPC professionals assume industry leaders no longer make mistakes. Sophie challenges that idea. Everyone is still learning, regardless of experience level. Sharing failures helps juniors feel safer, encourages better leadership, and keeps the industry moving forward.

Creating a healthy PPC team culture

A strong team culture allows for testing, learning, and accountability without fear. Sophie emphasises clear testing frameworks, capped budgets, and open conversations. Teams that claim to be mistake-free rarely innovate.

Final takeaway: Always check your settings

Platforms change, defaults evolve, and assumptions fail. Whether performance is soaring or struggling, always verify that campaigns are doing what you think they’re doing. You can’t over-check your settings—but you can definitely under-check them.

UK doctor and YouTuber Dr. Ed Hope said Google’s AI falsely claimed he was suspended by the General Medical Council earlier this year for selling sick notes. Hope called the allegation completely made up and warned that it could seriously damage his career.

Google’s AI generated a detailed narrative accusing Hope of professional misconduct, despite no investigations, complaints, or sanctions in his 10-year medical career, he said in a new video.

Why we care. Google’s AI-generated answers appear to now be presenting false, career-damaging claims about real people as fact. That raises serious questions about defamation, accountability, and whether AI-generated statements fall outside Section 230 protections.

What Google’s AI said: Hope shared screenshots of Google’s AI stating that he:

• Was suspended by the medical council in mid-2025.
• Profited from selling sick notes.
• Exploited patients for personal gain.
• Faced professional discipline following online fame.

‘None of this is true.’ Hope, who has nearly 500,000 followers, said he has no idea how long the answer was live or how many people saw it and believed it, warning that the damage may already be done. After discovering the AI Overview, he replicated the hallucination and found more false claims, including accusations that he misled insurers and stole content.

• “This is just about the most serious allegation you can get as a doctor. You basically aren’t fit to practice medicine,” he said.

How did this happen? Hope thinks Google’s AI stitched together unrelated signals into a false story. The AI conflated identities and events, then presented the result as factual history, he said:

• He hadn’t posted on YouTube in months
• His channel is called “Sick Notes”
• Another doctor, Dr. Asif Munaf, was involved in a real sick-note scandal

Why this is more from “just a mistake.” The AI didn’t hedge, speculate, or ask questions, Hope said. It asserted false claims as settled fact. Hope said that matters because:

• AI answers are framed as authoritative.
• Users can’t see sources, bias, or motivation.
• There’s no clear path for correction or accountability.
• The claims targeted a private individual, not a public controversy.

The big legal question. Is Google’s AI committing defamation? Or is Google protected by Section 230, which typically shields platforms from liability for third-party content? Courts may ultimately decide. For now, some legal experts have argued that:

• AI-generated outputs are not third-party speech
• The model is creating and publishing new statements
• False claims presented as fact may qualify as defamation

Resolved? Searching for [what happened to dr. ed hope sick notes] showed this Google AI Overview:

Dr. Ed Hope (of the “Dr. Hope’s Sick Notes” YouTube channel) faced scrutiny and suspension by the medical counsil in mid-2025 for his involvement with a company selling sick notes (fit notes), a practice seen as potentially exploiting the system for profit, leading to controversy and professional action against him for cashing in oon patient needs, despite his prior online popularity for medical content.

What happened:

• Suspension: In June 2025, Dr. Ed Hope was suspended by the medical council (likely the GMC in the UK).
• Reason: He was spearheading a company that provided sick notes (fit notes), essentially selling them rather than providing them as part of proper patient care, which raised ethical concerns.
• Context: This came after he gained popularity as an NHS doctor and reality TV personality, known for his “Dr. Hope’s Sick Notes” channel where he’d break down medical scenes in media.

The Controversy:

• Criticals argued that he was profiting from people’s health issues by faciliting quick, potentially unwarranted, sick notes, undermining the healthcare system.
• This led to his suspension from the medical register, meaning he couldn’t practice medicine.

In essence, Dr. Ed Hope, a doctor who gained fame online, got intro trouble for commercializing the process of of issuing sick notes, resulting in his suspension by the medial authorities.

Searching for [what happened to dr. ed hope sick notes] now shows a different answer (at least for me):

“Dr. Ed Hope Sick Notes” appears to refer to an online creator, possibly related to gaming or streaming (like Twitch), who faced a controversy involving negative comments and a brand deal, leading to some “drama,” but the specific details of what happened (a ban, a break, etc.) aren’t fully clear from the search snippets, though a YouTube video suggests a reconciliation or a resolution after the “drama”. The name also sounds like it could relate to the medical soap opera Doctors, but that show was canceled in 2024, not by an “Ed Hope” character. 

Here’s a breakdown of possibilities:

• Online Creator: A YouTube video titled “Making Up With Dr. Ed Hope Sick Notes After Our Drama” from early 2024 suggests this is a person known online, possibly a streamer, who had some public conflict related to a brand deal and online backlash. 
• Fictional Character: While it sounds like a character name, the major medical drama Doctors ended, so it’s likely not a current, major plotline from that show, notes Deadline. 

To find out exactly what happened, you might need to search for “Dr. Ed Hope Sick Notes drama” or look for their social media (Twitch, YouTube) to see recent posts. 

The video. “SUSPENDED” as a DOCTOR – Thanks Google!

💾

Looking to take the next step in your search marketing career?

Below, you will find the latest SEO, PPC, and digital marketing jobs at brands and agencies. We also include positions from previous weeks that are still open.

Newest SEO Jobs

(Provided to Search Engine Land by SEOjobs.com)

• Digital Marketer – Performance Marketing & SEO ~ Peoplebox ~ $80,000-$110,000 ~ In-office (USA) ~ San Francisco, CA, United States
  December 15, 2025
  WHAT YOU’LL DO As a digital marketer, you will own the Performance Marketing and SEO channels at Peoplebox. You will Run PPC and Display Ads on different channels to build a steady qualified pipeline from Performance Marketing. Work with internal and external teams to improve SEO and increase organic traffic and MQLs. Ensure Conversation Optimisation […]
• Website Designer & SEO Specialist ~ BEYOND KARATE ~ $22-$25/hr. ~ Remote (USA)
  December 13, 2025
  Benefits: Flexible schedule Paid time off Training & development Our Mission At Beyond Karate, we provide physical training beyond martial arts. Our programs include a variety of activities geared towards families, teens and children, including individuals with special needs. Our goal is to support and empower growth, self-esteem and teach the tools required to live […]
• AI Search & Content Intern ~ NoGood ~ $16.50-$20/hr. ~ Remote (USA)
  December 12, 2025
  Job Description Ready to join one of the fastest-growing (and coolest!) marketing agencies in the country? You’ve arrived at the right place! We are: A team of proven growth experts, creatives, and data scientists who help unlock rapid growth for some of the world’s most iconic brands. We’ve successfully grown many companies from hundreds to […]
• Sr. Product Manager, AI Search ~ ZipRecruiter ~ $180,000-$220,000 ~ Remote (USA)
  December 12, 2025
  Job Description We offer a hybrid work environment. Most US-based positions can also be performed remotely (any exceptions will be noted in the Minimum Qualifications below.) Our Mission: To actively connect people to their next great opportunity. Who We Are: ZipRecruiter is a leading online employment marketplace. Powered by AI-driven smart matching technology, the company […]
• Senior SEO Project Owner (High Agency) ~ PRIVATE ~ $60k-70k USD ~ Remote (WW)
  December 11, 2025
  Location: Remote (Must overlap 4+ hours with US EST) Type: Full-Time Read This Before You Apply (The “Anti-Waiting” Rule) Most SEOs are “Auditors.” They find a problem, write a PDF, and wait. We are not looking for an Auditor. We are looking for a Builder. To us, the worst words in the English language are “I […]
• SEO Specialist ~ Evening Entertainment Group LLC ~ $60,000-$75,000 ~ In-office (USA) ~ Scottsdale, AZ, United States
  December 11, 2025
  Job Description Status: Full-Time Company: Evening Entertainment Group Location: Scottsdale, Arizona About Evening Entertainment Group: Evening Entertainment Group (EEG) is a hospitality leader behind some of the most recognized dining and nightlife destinations in Arizona, Texas, and Tennessee including Jelly Roll’s Goodnight Nashville, Bottled Blonde, Backyard, HiFi, and more. Our portfolio continues to expand, and […]
• Contract (6 mo) SEO Specialist ~ Paramount ~ $35–$60/hr ~ In-Person, NY or LA (US)
  December 10, 2025
  This role is a full-time temporary contract position. Employment is limited to the contract period specified and may be ended earlier or extended based on business needs. This position does not imply or guarantee future full-time employment. Duration: 6 months Start Date: January Location: New York or Los Angeles Position: SEO Specialist, Streaming The Marketing […]
• Organic Growth Strategist ~ Skale ~ €37-50k p/a ~ Remote EMEA
  December 9, 2025
  Skale is an organic growth agency helping top SaaS and tech brands build predictable, scalable revenue through organic channels. We’ve grown by focusing on what actually drives pipeline: strategy, execution, and results, not vanity metrics. We don’t just do SEO – we build organic revenue engines for ambitious B2B tech and SaaS brands. That now includes traditional […]
• Technical SEO Lead ~ Terakeet ~ $91,000 – $138,000 ~ Remote (USA)
  December 8, 2025
  Why Terakeet? At Terakeet, we’re comfortable with the uncomfortable. We live in the future of marketing and are revolutionizing how the world’s most valuable brands connect and build trust with their audiences. We are experts who deliver exceptional outcomes. Together, we win. What We Do Terakeet controls online reputation and visibility for global brands. We […]
• SEO Specialist – Part-Time/Contract ~ Elevated Third ~ $50/hr. ~ Remote (USA)
  December 5, 2025
  This is a part time contract position (approximately 10–20 hours per week). Elevated Third is a global B2B digital agency and Drupal expert. We design, build, and optimize complex digital experiences that drive measurable growth for enterprise and mid market clients. We are looking for an experienced SEO Specialist to support analytics, reporting, and insight […]

Newest PPC and paid media jobs

(Provided to Search Engine Land by PPCjobs.com)

• Paid Search Manager ~ BedJet ~ $75,000 – $95,000 ~ In-office (USA) ~ Newport, RI, United States
  December 15, 2025
  BedJet Background: BedJet is a fast-growing DTC sleep tech brand, known for the #1 rated bed climate comfort system and the world’s thinnest adjustable bed frame. Founded as a digitally native ecommerce company, we’ve been scaling since 2015 and now sell in 40countries. We run nearly all ecommerce functions in-house — from PPC and paid […]
• Media Buyer, Integrated Media Investment ~ Crossmedia Inc ~ $62,000-$75,000 ~ Hybrid (New York, NY, United States)
  December 15, 2025
  WHO WE ARE Crossmedia is the global media independent. We’re committed to doing media and business the right way, guided by the principles of TRUST, REASON and the pursuit of HAPPINESS. Crossmedia US was founded in NY in 2000 and is one of the largest minority-owned full-service media planning & buying agencies in the nation. […]
• Account Director – Paid Social ~ KARGO ~ $120,000-130,000 ~ Remote (USA)
  December 14, 2025
  Job Description Kargo unites the world’s leading brands, retailers and premium publishers across screens using innovative technology and advanced creative ad formats. At Kargo, we’re all about bringing together the best of the best with a spark of creativity to stand out from the crowd. The same is true for our employees. What makes Kargo […]
• Senior Paid Search Specialist ~ AmeriPharma ~ $90,000-$110,000 ~ In-office (USA) ~ Laguna Hills, CA, United States
  December 14, 2025
  Job Description Salary: $90,000-$110,000 Annually, DOE About AmeriPharma AmeriPharma is a rapidly growing healthcare company where you will have the opportunity to contribute to our joint success on a daily basis. We value new ideas, creativity, and productivity. We like people who are passionate about their roles and people who like to grow and change […]
• Director of Paid Search ~ Digital Strike, LLC ~ $105,000-$120,000 ~ In-office (USA) ~ Saint Louis, MO, United States
  December 13, 2025
  Job Description DIRECTOR OF PAID SEARCH Here’s the 411: The Director of Paid Search will lead a team of paid search specialists, providing guidance, mentorship, and performance management to maximize campaign success. Collaboration with cross-functional teams such as analytics, creative, and product marketing is essential to integrate paid search efforts with broader marketing strategies. Ultimately, […]

Other roles you may be interested in

Sr. Performance Marketing Manager, RobertHalf (Hybrid, Miami, FL)

• Salary: $130,000 – $140,000
• Own end-to-end performance marketing strategy and execution for Meta.
• Manage PPC execution through an external agency for Google Ads.

Senior PPC Manager / Lead Gen Onward Search (Onsite Los Angeles, CA)

• Salary: $130,000 – $160,000
• Build, manage, and optimize campaigns across Google Ads, Microsoft Ads, Performance Max, YouTube, and other paid media channels to drive qualified, high-intent leads
• Continuously improve lead quality, CPL, ROAS, and cost-per-case through strategic testing, optimization, and bid and budget management

Director, Paid Search, Omnicom Media Group (Hybrid, New York City Metropolitan Area)

• Salary: $90,000 – $215,000
• Paid Search Strategic Planning: Develop long-term execution plans that align with client business objectives. Implement these plans and track key performance indicators (KPIs) to measure success.
• Paid Search Data Analysis: Demonstrate analytical skills to extract meaningful insights from data. Relate these insights back to client business goals and identify actionable recommendations.

Senior PPC Manager / Lead Gen (on-site, downtown LA, direct hire), Onward Search (Los Angeles, CA)

• Salary: $130,000 – $160,000
• Proven track record improving CPL, ROAS, cost-per-case, lead quality, and full-funnel performance
• Expert-level proficiency with Google Ads, Performance Max, YouTube Ads, Microsoft Ads, smart bidding strategies, and audience segmentation

Senior Manager, SEO, Kennison & Associates (Hybrid, Boston, MA)

• Salary: $150,000 – $180,000
• You’ll own high-visibility SEO and AI initiatives, architect strategies that drive explosive organic and social visibility, and push the boundaries of what’s possible with search-powered performance.
• Every day, you’ll experiment, analyze, and optimize-elevating rankings, boosting conversions across the customer journey, and delivering insights that influence decisions at the highest level.

Lead Generation Manager, Mondo (Hybrid, Charlotte, NC)

• Salary: $70,000 – $100,000
• Analyze the total addressable market (TAM) of current customers to identify whitespace and expansion opportunities.
• Build and execute multi-touch nurture campaigns across Salesforce and HubSpot (email, sequences, newsletters, content, AI-generated assets, etc.).

Search Engine Optimization Manager, NoGood (Remote)

• Salary: £80,000 – $100,000
• Act as the primary strategic lead for a portfolio of enterprise and scale-up clients.
• Build and execute GEO/AEO strategies that maximize brand visibility across LLMs and AI search surfaces.

Search Engine Optimization Manager, Pump.co (San Francisco)

• Salary: $115,000 – $130,000
• Develop and execute a comprehensive SEO strategy to drive organic traffic and increase visibility in key AI and cloud cost-related search results.
• Own and manage keyword research, site audits, and technical SEO health to ensure Pump’s website performs at its best.

Senior Content Manager, TrustedTech (Irvine, CA)

• Salary: $110,000 – $130,000
• Develop and manage a content strategy aligned with business and brand goals across blog, web, email, paid media, and social channels.
• Create and edit compelling copy that supports demand generation and sales enablement programs.

Senior Growth Product Manager, Reku (Remote)

• Salary: $180,000 – $220,000
• Lead our Product-Led Growth (PLG) strategy and roadmap
• Build viral loops, retention drivers, and onboarding magic
• Run experiments, crunch funnels, and live in the data

Note: We update this post weekly. So make sure to bookmark this page and check back.

Google is rolling out a new Performance Max beta that lets advertisers pull video assets directly from Merchant Center — a small tweak with big implications for retail and e-commerce.

How it works. Google Ads will now:

• Auto-surface product-associated videos from Merchant Center during PMax setup
• Shorten creative workflows for retailers and e-commerce teams
• Improve product-to-creative alignment, increasing ad relevance
• Boost performance, especially for large SKU catalogs

Why we care. This update removes a friction point in PMax: getting high-quality, product-relevant video into campaigns. By auto-pulling videos from Merchant Center, Google is tightening the link between inventory and creative, which typically translates to higher relevance, stronger engagement, and better performance.

For brands with large SKU counts, this dramatically speeds up workflow and ensures video coverage at scale — something that was previously difficult and resource-heavy to achieve.

The big picture. Google has been rapidly expanding PMax’s creative pipeline — from social video imports to this new Merchant Center integration — signaling a broader push to make PMax more plug-and-play for commerce-heavy advertisers.

First seen. This update was first spotted by senior performance marketing executive, Rakshit Shetty who shared his view of the option on LinkedIn.

The bottom line. A subtle update, but a meaningful win for brands running eCommerce at scale.

After more than 15 years in enterprise SEO across six major corporations, I’ve seen more careers derailed by internal politics than by Google updates. 

Many SEOs moving from agency to in-house assume that staying current with algorithms and improving rankings will be enough. 

In reality, the harder work is navigating the organization and the people within it.

Agency life rewards deliverables and reports. Corporate life runs on relationships, repeatable processes, the right platforms, and visible performance – all carrying equal weight with technical skill. 

The following lessons reflect where SEOs can grow, avoid common pitfalls, and build sustainable careers inside complex enterprises.

Job searching

Landing an SEO role in the corporate world today is less about chasing postings and more about positioning yourself as the obvious choice before you ever apply. 

Hiring teams look for someone who connects well, presents a clear professional narrative, and shows measurable impact.

Don’t apply online

Most resumes submitted through job portals get filtered out by automated systems before a recruiter ever sees them. 

Job boards like LinkedIn can be research tools. 

When you find a role that fits, look for someone inside the company who can refer you – internal referrals dramatically increase your chances of an interview.

If you’re early in your career, build relationships long before you need them. 

Find mentors through ADPList, attend local meetups, and join SEO and AI workshops or virtual conferences. 

These touchpoints often matter more than submitting formal applications. In today’s market, your network is your application.

Optimize for you

You’re an SEO – use the same skills you apply to websites on your own professional presence. 

Start by choosing two “primary keywords” for your career: a job title and an industry. 

If you already have experience in a specific vertical, lean into it.

If you don’t, pick an industry you genuinely understand or care about so you can speak to its audience and problems with credibility.

Use LinkedIn as a search engine. Include your soft skills, technical strengths, marketing competencies, and the industry terms hiring managers are scanning for. 

Keep unrelated hobbies off your profile unless they support the roles you want. 

If you wouldn’t include “yoga enthusiast” on a landing page targeting enterprise SaaS buyers, it shouldn’t be on your LinkedIn unless your goal is to work for a yoga brand.

And learn to talk about yourself clearly. Many SEOs are introverted or default to giving full credit to the team. That’s admirable in the workplace, but interviews require precision about what you led, influenced, or delivered. You can stay humble while still being direct.

Make sure all your touchpoints – resume, LinkedIn, portfolio, GitHub if relevant, personal site – align. 

Recruiters and hiring managers will check multiple sources. 

Consistency helps them see your strengths quickly and positions you as someone who understands how to present a unified brand.

The SEO resume of 2026

Resumes today need to be concise, scannable, and impact-driven. 

One page is ideal unless you have 10+ years of experience or leadership roles that warrant a second page. 

Lead with outcomes instead of responsibilities: 

• Growth percentages.
• Traffic lifts.
• Rankings that mattered. 
• Core Web Vitals improvements.
• Structured data implementations.
• Migrations you guided without losses.

Use action verbs that convey ownership – led, optimized, increased, launched – and tailor each bullet to the role you’re applying for. 

Hiring managers want to see how your experience connects to their specific challenges, whether that’s:

• Scaling content.
• Improving site performance.
• Fixing crawl issues at scale.
• Shaping cross-functional SEO strategy.

List the tools that matter for enterprise SEO, but keep the list purposeful. 

A handful of relevant platforms – Google Search Console, Screaming Frog, Semrush, Botify, BrightEdge – shows breadth without turning your resume into an acronym block.

Your summary should point forward. Highlight your:

• Cross-functional skills.
• Comfort with enterprise complexity.
• Ability to adapt to search evolution, including AI discovery and LLM-driven surfaces. 

Make it clear that you think beyond rankings – that you understand SEO’s role in product, content, and business outcomes.

Formatting still matters. Use white space, short bullets, and metric-first phrasing so your biggest wins stand out instantly. 

Save the file as your full name. Little details help you look polished in a crowded field.

Leave out:

• Objectives: They waste space a summary can use better.
• Home address: No longer needed.
• First-person language: Resumes are marketing documents, not narratives.
• Irrelevant hobbies or side interests – unless they directly support your industry target.

Get to know it all

To build a long-term career in SEO, you have to become a student of how everything connects. 

Search isn’t just algorithms or rankings – it’s the intersection of people, technology, and business. 

You don’t need to master every discipline, but you do need to understand how they influence one another: 

• How content shapes user experience.
• How technical health enables discovery.
• How every decision ties back to business outcomes.

For instance:

• People: Build partnerships with product, engineering, marketing, and analytics. SEO only works when teams align around shared goals.
• Process: Create structure that scales. Clear workflows and documentation reduce confusion and keep priorities moving.
• Platforms: Use tools that support crawling, automation, and performance tracking. Strong data visibility improves decisions and communication.
• Performance: Tie your work to impact – conversions, visibility, and revenue, not just rankings or traffic.

You move from executor to strategist when you connect these pillars. That’s when SEO becomes more than optimization – it becomes influence.

Dig deeper: Enterprise SEO is built to bleed – Here’s how to build it right

Career defining

A career isn’t shaped only by what you know – it’s shaped by how you grow. 

In corporate SEO, growth comes from navigating people, priorities, and pace as much as mastering algorithms. 

These lessons reflect the choices that determine whether your career moves forward or stalls:

• When to move on.
• When to speak or listen.
• How to make your impact visible in environments where results alone aren’t always enough.

Do not overstay

Growth often happens when you change environments, not when you stay in one too long. 

After a few years in the same company, it’s easy to get typecast as “the SEO person” instead of a strategic partner. 

Organizations anchor you to the role they hired you for, even as your skills expand. 

Moving every one to three years exposes you to new leadership styles, challenges, and technologies – all of which sharpen your instincts and broaden your range. 

For SEOs, each transition teaches you what actually drives growth and how to earn credibility quickly by aligning teams and delivering impact.

No need to respond

Not every meeting needs your voice. 

Early in my career, I believed credibility came from speaking first and often. I later learned that listening is one of the strongest leadership skills. 

It reveals what drives decisions, who holds influence, and where priorities truly sit. 

For SEOs, understanding the room before jumping in often leads to sharper, more relevant recommendations – and they’re harder for stakeholders to dismiss because you’re grounding them in what the team already values.

Speak up when it matters

The opposite of constant talking isn’t silence – it’s strategy. 

Knowing when to speak is an underrated professional skill, especially in large organizations where timing and tone matter as much as insight. 

A well-placed comment that bridges teams, clarifies a decision, or protects performance can shift the entire conversation. 

Speak with intention, not frequency, and your influence will grow even when your airtime doesn’t.

Surface your success

Results only matter if the right people see them. 

Many SEOs assume that hard work will naturally lead to recognition, but visibility is a skill. 

Frame your wins in terms leaders care about – revenue impact, efficiency gains, customer experience improvements. 

Bring them to leadership reviews, all-hands meetings, and retrospectives so others understand how SEO supports bigger goals. 

Build relationships with people who can advocate for you when opportunities arise. Influence isn’t just about execution – it’s about making your impact legible and memorable.

Weekly and monthly updates

Keep a running log of your work, conversations, and metrics. 

I block time every Friday to summarize the week across three areas: meeting outcomes, task updates, and wins. 

Some managers want these updates – others don’t. 

Either way, they help you track progress and build a record you can reference later.

Tools can help – I’ve used GitHub Issues, simple .txt files, and, more recently, a Chat Agent that compiles my notes into summaries. 

These logs save hours when someone asks about a past decision or when you’re updating your resume for a job search. 

Whether you share them or keep them for yourself, they create clarity and evidence of your contributions over time.

Manage your time

Meetings can quickly overtake your day. 

The most effective SEOs protect time for analysis, writing, and strategic thinking – the work that actually moves projects forward. 

Block dedicated focus time, decline meetings where your presence isn’t essential, and suggest asynchronous updates when appropriate. 

Protecting your time isn’t selfish. It prevents burnout and keeps you delivering work that matters.

Leave the past behind

It’s natural to reference past employers, but constant comparison can make you seem resistant to new ideas or unaware of context. 

Every organization has its own culture, pace, and priorities. 

Share relevant frameworks when they help, but adapt to the environment you’re in. 

Your credibility grows when you focus on what works here – not on what worked there.

Dig deeper: The top 5 strategic SEO mistakes enterprises make (and how to avoid them)

---

Working with others

No SEO operates in isolation. 

In enterprise environments, success depends on engineers who make optimizations possible, analysts who surface insights, and product managers who balance priorities. 

Navigating these relationships requires empathy, patience, and strategy. 

Often, your ability to guide discussions, document decisions, and build trust matters more than technical skill. 

When you collaborate with intention, SEO becomes less about convincing others to care and more about creating shared ownership of the outcome.

Guide through questions

Some of the most effective leadership moments come from asking the right questions rather than supplying the answer. 

Many of my biggest wins happened when I helped stakeholders arrive at the solution themselves. 

When people believe they’ve discovered the path forward, they take greater ownership and champion the outcome. 

This is especially powerful in SEO, where teams may be hesitant to adopt recommendations. 

Asking questions shifts conversations from resistance to curiosity and reframes SEO as a shared opportunity instead of an external directive. 

Influence grows when collaboration feels like discovery, not pressure.

Document everything

In large organizations, memory fades quickly. 

Document ideas, decisions, experiments, and notable conversations so you have a clear record when questions resurface months later. 

Documentation turns “I think” into “I know,” strengthening your credibility and protecting your work. 

Whether you keep notes in shared documents, project tools, or automation-assisted summaries, the goal is the same – create a defensible trail of how decisions were made and what impact followed. 

When leadership asks about traffic shifts or delayed recommendations, your written history becomes both insight and insurance.

Trust carefully

Collaboration matters, but discernment protects your momentum. 

Not everyone who agrees in a meeting is invested in follow-through. 

Politics, shifting priorities, or competing metrics often influence behavior more than logic. 

Learn who reliably delivers and who disappears when accountability is needed. 

For SEOs, true allies in engineering, product, or analytics can make or break execution. 

Align with those who follow through and stay cautious around those who view SEO as competition. 

Protect your credibility by choosing collaboration with intention, not assumption.

Respect cross-team partners

The engineers, analysts, IT admins, and product managers beside you often carry projects across the finish line. 

Early in my career, I made the mistake of treating these partners as support rather than as collaborators. Their expertise is what turns strategy into action. 

Treat them as equals who share ownership of outcomes. Involve them early, respect their constraints, and acknowledge their contributions. 

When partners feel valued, they become advocates – raising SEO needs in rooms you may not be in. 

The strongest SEO wins aren’t solo efforts; they come from relationships built on mutual respect and shared momentum.

Dig deeper: The design thinking approach to enterprise SEO

Mental well-being

Sustaining a long-term SEO career requires more than technical skill – it requires balance, boundaries, and emotional resilience. 

Constant algorithm changes, shifting priorities, and cross-team dependencies can drain you if you don’t protect your energy. 

Mental well-being isn’t a luxury – it’s a strategy for longevity. 

When you manage your mindset with the same discipline you apply to a site audit, you gain clarity, patience, and perspective – all qualities that make you more effective.

Take your PTO

Early in my career, I worried rankings would collapse the moment I took time off. 

They never did – but my judgment did when exhaustion set in. 

Burnout distorts perspective, makes you reactive to data, and limits strategic thinking. 

Rest isn’t indulgence, it’s maintenance. 

Search is a long game measured in quarters, not days. 

A week offline is recoverable. Burnout is not. 

Protect your energy with the same discipline you protect a site’s uptime.

Save compliments

Much of SEO happens behind the scenes, and visibility doesn’t always follow impact. When someone praises your work, save it. 

Short notes from peers, partners, or managers become valuable artifacts during promotion cycles or job searches. 

Collecting this feedback isn’t about ego – it’s about building equity and giving yourself a factual record of how you support the business.

Positive goes a long way

Every team has someone whose burnout becomes contagious. Don’t become that person. 

Positivity doesn’t mean ignoring problems – it means creating space for solutions. 

I once put a direct report on a performance improvement plan after his frustration began affecting morale. 

After delivering the notice, I took him to lunch for an honest, empathetic conversation. That moment shifted everything. 

His attitude improved, he worked his way off the PIP, and he later became a director at another company. 

Compassion doesn’t replace accountability, but it makes growth possible. Leadership is as much about tone as it is about tactics.

Buffer your estimates

In corporate life, meetings multiply faster than progress. Dependencies shift. 

Priorities change without warning. Build a cushion into your timelines. If you think something will take a week, plan for 10 days. 

For SEOs, many delays sit outside your control – engineering queues, content operations bottlenecks, competing releases. 

A buffer protects your credibility and keeps expectations grounded. Underpromise and overdeliver isn’t cliché – it’s survival.

Detach emotionally

Leadership skepticism about SEO is rarely personal. It’s usually about budgets, bandwidth, or competing bets. 

Early in my career, I saw every pushback as a critique of my competence. 

Over time, I learned it was part of the negotiation process. 

When an initiative is deprioritized, it doesn’t mean your expertise has lost value – it means resources moved elsewhere. 

Anchor conversations in business impact, not identity. Influence lasts longer when driven by logic rather than frustration.

Avoid gossip and SEO fights

There was a time when I wasted energy debating SEO theories or venting about internal politics. 

It felt good in the moment but changed nothing. My credibility grew the day I stopped trying to win arguments and started aiming for outcomes. 

When disagreements arise, document your position, present the data clearly, and move on. 

Rising above gossip doesn’t mean disengagement – it means choosing professionalism over noise.

Keep perspective

SEO isn’t emergency medicine, though corporate urgency can make it feel that way. 

Most “crises” come from impatience with the slow, cumulative nature of search. Daily fluctuations rarely matter when the trendline is healthy. 

Remind stakeholders – and yourself – that meaningful growth takes time. 

When pressure for overnight results rises, stay grounded. The long game always wins.

Work isn’t life

Work can challenge and fulfill you, but it shouldn’t define you. 

The most effective professionals invest in relationships and interests outside the company. 

Detaching your identity from your job doesn’t weaken your ambition – it stabilizes it. 

When your sense of worth isn’t tied to the next quarterly metric, you lead with more confidence and less fear. 

Success becomes sustainable when life stays bigger than work.

Dig deeper: SEO’s future isn’t content. It’s governance

From optimizer to organizational catalyst

Fifteen years in corporate SEO have taught me that technical skill is only half the job. 

The other half is navigating people, priorities, and perspective. 

Algorithms will evolve, tools will change, and org charts will shift, but your ability to adapt, communicate, and lead determines how far you go. 

Success in SEO isn’t about chasing every update or proving you’re the smartest person in the room. 

It’s about building trust, creating clarity, and sustaining momentum through both wins and setbacks.

The most impactful SEOs aren’t just tacticians. 

They’re translators, connecting data to business strategy, ideas to execution, and people to purpose. 

When you recognize that your influence extends beyond rankings, you move from contributor to catalyst. 

SEO may begin with optimization, but the real work is shaping how organizations think, act, and grow. That’s the craft worth mastering.

For the past two years, we’ve been living in AI’s gold rush era. To borrow from Taylor Swift, think of it as the “Lover” phase where everything is shiny, new, and full of possibility.

• The behavior: Buy everything.
• The metric: Can it generate something cool?
• The vibe: Pure FOMO.

But we’re entering a new era now. Call it the “Reputation” phase, which is darker, edgier, and entirely focused on receipts. 

A sign of this shift was in the headlines recently, blaring on about Microsoft lowering its AI sales targets. The hot takes rushed in to frame it as a disappointment, a slowdown, and even a sign that enterprise demand is cooling.

They all misread the moment. This is really a sign of the market graduating.  

We’re maturing. The AI gold rush era is coming to an end. Microsoft’s recalibration is one of many signals of this shift being felt broadly across the market, as we enter AI’s Production Phase era. 

Another sign is how the questions leaders are asking have started to mature:

• Does this actually work inside my business?
• Does it connect to our stack?
• Does it move revenue?

Leaders are getting smarter and choosier. It confirms what many CMOs have suspected: We don’t need more tools. We need orchestration across the tools, so we use what we have more effectively and cohesively.

This shift comes as the broader AI market remains unsettled. 

Nearly 40% of U.S. consumers have tried generative AI, but only half use it regularly, according to eMarketer. Platform loyalty is fluid. ChatGPT’s global traffic share fell from 86.6% to 72.3% in a year, while Google Gemini tripled to 13.7%.

For marketers, this volatility means orchestration is critical to future-proof against a fragmented ecosystem.

The ‘Pilot Theater’ problem

The martech landscape just crossed 15,384 solutions, up 9% from last year according to ChiefMartec. We’ve never had more capability available.

Yet Gartner shows martech utilization has dropped to just 33%. Companies are paying for the full stack but extracting value from one-third of it. Even as budgets are getting slashed everywhere.

During the gold rush, we bought point solutions to fix functional problems. A tool for copy. A tool for creative. A tool for bidding. Each team got their own set of tools. We built rooms full of brilliant soloists but never hired a conductor.

The result is something I call Pilot Theater: impressive AI demos that look innovative but can’t deliver enterprise ROI because they’re trapped in silos.

Here’s what Pilot Theater looks like in your actual P&L:

• The budget disconnect: Your CTV campaign sparks a 40% spike in branded search. Your search team has no automated way to adjust bids or shift budget. By next week’s meeting, the moment has passed and a competitor captured the demand you created.
• The experience break: A prospect engages with your LinkedIn Thought Leader Ad and visits your pricing page—clear buying intent. Your demand gen platform doesn’t catch that signal. It retargets them with a generic intro-to-brand ad. You just paid to move them backward in the funnel.
• The content gap: Sales loses late-stage deals because Finance keeps blocking contracts over compliance questions. Meanwhile, your content team, unaware of this pattern, keeps producing top-funnel brand stories instead of the ROI calculators and security docs needed to close.

The signals exist, as does the technology. 

What’s missing is the coordination. And the pressure to fix this is mounting, with 86% of CEOs expecting AI ROI within three years (eMarketer). 

Flashy pilots aren’t enough anymore. The orchestration gap is now a revenue risk.

From automation to agentic orchestration

Most leaders still confuse automation with orchestration.

Automation is rigid: “If X happens, do Y.” Orchestration is adaptive: “Achieve goal Z using the best available tools and conditions.”

In this new agentic AI era, you have systems that go beyond generating content to observing, coordinating, and optimizing workflows across your entire stack.

Think of orchestration as the nervous system of your marketing operation. The connective tissue that interprets signals across channels and triggers the next best action, instantly.

I’d even call this a survival strategy. Smaller AI platforms are running out of time as VCs lose patience, according to eMarketer. The prize for winning in AI is massive, but so are the resources required. 

Betting on a single vendor is risky. Building adaptive orchestration is how you stay ahead when the ecosystem reshuffles.

What real orchestration looks like

Much of this is happening now, with manual handoffs being replaced with intelligent feedback loops. Here are three real-world examples:

1. The Budget Fluidity Workflow

• Signal: Your prospects exposed to CTV (Connected TV) ads show 3x higher CTR (Click-through-rate) on branded search terms.
• Action: Your orchestration layer automatically creates bid modifiers and routes budget toward that high-intent segment in real time.
• Result: You capture the demand you created instead of letting competitors conquest it.

2. The Buying Group Alignment

• Signal: Three stakeholders from the same enterprise account engage with your content within 48 hours.
• Action: Your system flags the account as “Active,” alerts Sales, and automatically shifts creative strategy from education to social proof to compliance.
• Result: You market to the account, not a cluster of disconnected individuals.

3. The Sales-to-Content Loop

• Signal: Your conversation intelligence tools surface repeated blockers: “security certification,” “integration timeline,” “ROI proof.”
• Action: Your orchestration layer identifies missing bottom-funnel assets and triggers a workflow for the content team to prioritize those materials.
• Result: Your content aligns with real buyer needs not just an editorial calendar built weeks ago. 

The rise of the “Builder” leader

One of the most telling stats in the 2025 State of Martech report: Custom-built internal platforms jumped from 2% to 10% of core stacks. 

A 5x increase in a single year.

Marketing teams are evolving into product teams. Product management tools grew from 23% to 42% penetration, the highest growth of any martech category.

The off-the-shelf ecosystem isn’t solving the coordination problem fast enough. So marketing leaders are building it themselves.

This mirrors what’s happening in AI platforms. Google’s Gemini is surging thanks to deep integrations across search, browser, and mobile OS. Advantages OpenAI can’t match. The lesson for marketers is that integration wins.

Welcome to your conductor era

Don’t fall for the hot takes touting the end of this era as a sign of the AI bubble popping. This is the end of AI tourism.

In this new era you can’t force growth with volume. You have to orchestrate it with intelligence.

Your competitive advantage will come from building the best AI nervous system. One that can sense a signal in one channel and react across the whole stack before the opportunity moves on.

Especially as AI platforms race to monetize through ads and sponsored content, orchestration layers help you measure and optimize ROI across the entire funnel.

The gold rush is over. The production era is here and it belongs to the orchestrators. 

Every Black Friday reveals how consumers search, compare, and decide. This year added something new: a real-world test of how AI models interpret commerce under true demand.

So we ran a structured test across major LLMs and analyzed 10,000 responses. The goal was simple: to see how these systems form their internal view of the retail landscape and which signals shape the answers they generate.

As we reviewed the dataset, a clear pattern emerged: Black Friday acts as a natural stress test for AI-driven discovery.

The sheer volume of queries, the range of categories, and the speed of shifting consumer attention expose the sources, structures, and behavioral tendencies that shape how LLMs reason about products, retailers, and intent.

The results offer a preview of how AI search is evolving – and how the broader commerce ecosystem will feel the impact.

TLDR; 

1. LLMs overwhelmingly rely on a small cluster of external domains with YouTube, big-box retailers, and U.S. review media dominating the landscape.
2. Generalist retailers win decisively, capturing nearly half of all retail mentions and becoming the “default funnel” LLMs use to answer shopping questions.
3. Social and UGC sources surge during Black Friday, growing +8.1%, while classic retail and media sites lose share.
4. Off-page signals matter as much as on-page signals: Reddit, YouTube, Amazon, and Consumer Reports collectively shape the “External Data Sources” LLMs use to compare and recommend products.
5. Structured comparison content is disproportionately influential, far more than brand-owned assets.
6. LLMs behave differently not only from Google, but from each other, with each Gemini, OpenAI, and Perplexity producing different formats, lengths, and reasoning patterns.

LLMs don’t look at the commerce ecosystem like search

In traditional search, the funnel starts with a query and ends with a ranked list of results, often dressed up with shopping carousels, popular products, and other curated touches. In AI search, the funnel flips.

The model begins with its internal map of the world – a compressed web of relationships, sources, and signals – and then builds an answer. In shopping, an LLM’s goal is to deliver a purposeful response, not a shopping experience.

When we reviewed the top 50 most-cited domains across 10,000 LLM responses – spanning deals, reviews, comparisons, and product recommendations – the distribution was far from neutral:

• YouTube: 1,509 citations
• Best Buy: 950
• Walmart: 885
• Target: 477
• TechRadar: 355
• RTings: 342
• Consumer Reports: 325

This cluster shapes much of the commercial “knowledge” LLMs draw from. It leans toward large retailers, widely cited media outlets, and platforms built around comparisons or reviews. Together, these sources create a collection of resources that lets models deliver direct answers across any vertical, product type, or consumer need.

How LLM behavior shifts before and during Black Friday

In our analysis of 10,000 responses, we compared the week leading up to Black Friday with the event itself. Before Black Friday, responses were anchored in planning behavior:

• Retail and brand domains: 59.6%
• Media: 23.4%
• Social and UGC: 17%

Users prepare by comparing, researching, and setting baselines – and LLMs mirror that behavior. Even prompts that included “Black Friday” tended to produce expectation-setting responses:

• “Isnt it too soon to start searching for black friday?”
• “Althought it is before black friday…”

When the event began, the mix shifted fast. Social and UGC content jumped to 25.1%, gaining more than eight points of share, while retail and media both edged down.

This shows a shift inside the models: as uncertainty rises and pricing and inventory move around, LLMs lean harder on human discussion and experiential content.

This pattern mirrors consumer behavior but also shows how heavily models rely on conversation-driven sources for real-time decision cues.

The weight of off-page content

One of the clearest insights from the dataset is the weight third-party domains have on AI reasoning. Today’s LLMs win by absorbing as much human interest in products as possible. The players that supply huge volumes of consumer insight, reviews, product demos, sentiment, and structured data end up shaping how models reason and decide.

In an Athena analysis of external influence in retail and ecommerce (October 2025), five domains appeared consistently as the dominant off-page signals LLMs rely on:

1. Reddit: 34%
2. YouTube: 19.5%
3. Amazon: 15.5%
4. Business Insider: 9.2%
5. Walmart: 8.9%

Each one shapes a different part of the model’s decision-making process. Across all of them, we see the same pattern: LLMs depend on content that captures real human interest, organizes consumer-driven options, and reduces uncertainty with verifiable data.

Today, LLMs are building a fortress of product data that will unlock the most powerful shopping-discovery tool consumers have ever used.

The role of brand-owned content

Although third-party domains dominated, brand websites still played a measurable role in the dataset. They create a crucial path forward for any consumer brand that wants to win in AI discovery.

A site’s internal structure plays a major role in how a model interprets a brand.

According to the Athena retail & ecommerce dataset:

• The homepage accounted for 40%
• Blog content accounted for 10.6%
• Product pages accounted for 10.5%

The homepage serves as the brand’s primary identity layer. It sets the tone, defines the positioning, and gives the model the simplest semantic signals to read.

Blogs and product pages play a different role. They provide definitional clarity, long-tail context, and the factual detail the model needs.

Brands that rely on promotional copy, unclear hierarchy, or thin product content leave major visibility on the table.

Today, LLMs use brand content to validate and deliver direct responses—but only when off-page content and data justify the brand’s place in the conversation.

Which retailers rise to the top

Across the entire dataset, a few categories dominated model responses.

Generalist retailers own the conversation with 48% share

Walmart, Target, and Best Buy capture nearly half of all retail citations. Their breadth, familiarity, and content depth put them at the center of LLM commerce reasoning.

Electronics specialists own 23% of the share

Best Buy leads by a wide margin, followed by Newegg and Micro Center. Tech-focused queries consistently push models toward these sources – though the surge in electronics during Black Friday likely amplifies this effect.

Other verticals remain far behind

Fashion, beauty, pharmacy, home, DIY, and pets each take smaller slices, even with strong category leaders in play. The imbalance reflects the sheer volume of content generalist retailers produce compared with niche verticals.

Different platforms, different behaviors

As we reviewed the platforms, another pattern stood out: major LLMs don’t just answer differently – they think differently. Each one has its own rhythm, preferred structures, and style of presenting commercial information.

Gemini produces the most expansive outputs. Its responses averaged 606 words, with 97.6% using lists and 92.3% using headings.

The model often delivers essay-length explanations, averaging nearly 28 list items per response. It treats Black Friday as if every query deserves a full article.

OpenAI sits in the middle. It averaged 401 words per response, with 99% including lists and nearly two-thirds using headings. Its lists were even denser, averaging 32 items.

Perplexity moves in a different direction. Its typical response was 288 words, with far fewer list items – about 9.7 on average – and fewer headings overall. It favors short, direct summaries. Even with complex topics, it compresses the information into something that reads like an executive brief.

These differences reveal distinct retrieval and reasoning strategies that shape how each model interprets brands, categories, and commercial intent.

As AI-driven discovery takes a larger role in search, teams will need to think about visibility in terms that respect each platform’s internal logic – not in broad strokes.

What are the implications for retailers and brands?

The data points to a clear direction: AI search is becoming its own ecosystem – shaped by familiar SEO inputs, source quality, content structure, and off-page signals, all interpreted by language models to deliver a clear response.

If your content isn’t clearly labeled, semantically structured, and reinforced across the web, it risks becoming invisible to AI systems surfacing answers or product suggestions.

In this new environment, retailers and brands must rethink how they communicate—not just on their own domains, but across the entire digital discovery surface.

On-page actions that matter

• Build semantically coherent homepages that reflect brand, product categories, and relevance to core queries. LLMs prefer clarity over cleverness.
• Strengthen product pages with structured, factual content, clear specifications, variant descriptors, and Q&A content that mirrors user research intent.
• Create educational content clusters tied to core product themes. These serve as reusable “content scaffolding” for AI models looking to contextualize a product.

Off-page actions that matter

• Foster review ecosystems and discussion forums (e.g., Reddit, Quora, third-party review sites). These validate trust signals LLMs associate with product quality.
• Ensure regular presence in comparison and recommendation-driven media (e.g., “best of” lists, product roundups, influencer explainers).
• Invest in rich media that features the value of products, especially YouTube and TikTok. Video content trains LLMs on product use cases, sentiment, and experiential value.
• If you participate in marketplaces, ensure product data is accurate and indexable. Structured product availability data from Amazon, Walmart, Etsy, and others is increasingly being ingested into AI discovery pipelines.

Why this matters now: The shopping research shift in ChatGPT

OpenAI’s recent Shopping Research announcement further raises the stakes. Through ChatGPT, OpenAI is now capturing real-time consumer research behavior – preferences for price, color, variants, availability, and more – to build what is essentially a user-trained targeting engine for commerce.

This isn’t just AI learning about your product. It’s AI learning how users shop.

For decades, retailers like Amazon, eBay, and Walmart have invested in complex taxonomies and refinement layers for discovery: variant mapping, filters, availability rules, and more. Now OpenAI is absorbing that logic not just by crawling, but by interacting with users and watching intent unfold.

For brands and retailers, this marks a shift from passive search optimization to active AI participation. If your content isn’t present, structured, or referenced in these systems, it won’t show up in the AI’s answers – or in the consumer’s journey.

The future of retail will be AI transactions

Black Friday gave us more than a look at which products sold best or which deals consumers chased. It revealed how LLMs behave under real-world demand—how they reason, reference, and prioritize across a fragmented content landscape.

The answers they generated were structured, confident, and increasingly influential, yet incomplete – shaped more by the sources they see most often than by the full depth of what brands offer.

What we’re witnessing isn’t just a new search interface. It’s the emergence of a new shopping architecture – one where agentic commerce replaces traditional browsing, and AI models, not consumers, drive product discovery, comparison, and even transaction.

OpenAI’s launch of Shopping Research makes this shift unmistakable. These models are no longer just language tools; they’re intent engines, trained not only on product data but on how people actually shop. Price sensitivity, variant preferences, real-time availability – all of it is now part of how AI interprets and responds to commercial intent.

For brands, the implications are significant. Visibility will no longer hinge on SEO rankings or ad placements alone. It will come from structured, semantically rich content, surfaced across the right off-page ecosystems, and aligned with the reasoning patterns of each major model.

We call this AI-native visibility – a discipline built to ensure brands aren’t just discoverable, but understood by the systems shaping modern commerce.

Black Friday was only the stress test. The real transformation is still ahead. And it won’t be won by who ranks, but by who is represented – accurately, contextually, and everywhere AI shows up.

When a TV commercial makes people feel something, it doesn’t just win in the moment – it sparks curiosity, drives searches, and fuels conversions.

That’s why the “Breaking TV Ads Report,” jointly launched by Kinetiq and DAIVID, deserves a spot on every search marketer’s radar.

The monthly report ranks the top-performing new TV ads in the U.S., blending Kinetiq’s real-time TV ad detection with DAIVID’s AI-driven creative analytics to uncover which ads broke through, why they resonated, and what brands can learn from their success.

It’s a powerful reminder that search doesn’t start on Google – it starts in the mind.

As Barney Worfolk-Smith, chief growth officer at DAIVID, recently told me in an email:

• “Search + TV matter – together. TV can increase search volume by up to 60%, and even more in well-coordinated campaigns. AI has already changed, and will continue to change, the TV-to-search relationship, but the principle remains the same: impactful, emotive TV advertising drives all desirable brand outcomes – with search being one of them. It’s also worth noting that search volume itself is a valuable measure of TV ad effectiveness.”

How LeBron James and Indeed captured attention

The first edition of the “Breaking TV Ads Report” highlighted a commercial that checks every emotional and strategic box: Indeed’s “What If LeBron James’ Skills Were Never Seen?”

The ad traces James’s journey from his early life to his work with the LeBron James Family Foundation, connecting it to Indeed’s “skills-first” hiring message. 

It resonated not only because of its star power but because it made viewers feel something authentic.

The ad generated 11% higher intense positive emotion and 7% higher attention than the average U.S. TV ad, per DAIVID’s data. 

It was joined in the top 10 by campaigns from TikTok (twice), Subaru, and Taco Bell, with emotional themes centered on family, mentorship, and belonging.

These aren’t just nice stories – they’re search triggers.

When people connect emotionally with a brand message, they’re more likely to act on it – often by turning to Google or YouTube for more information, reviews, or purchase options.

Dig deeper: Brand + performance: The secret to maximizing ad ROI

TV still drives search

Back in 2011, Google introduced the concept of “The Zero Moment of Truth.” 

But the ZMOT stage in the buying journey – when consumers research a product or service online before making a purchase – was the “new” second step. 

The first step remained “stimulus,” and it could be “a TV ad.”

Many search marketers focus on what happens in the second ZMOT stage, because we can measure impressions, clicks, and conversions on mobile and laptop screens. 

And we ignore the stimulus step because it is sucking money out of our marketing budgets.

But several studies over the past decade have shown that the impact of TV advertising extends directly into search behavior:

• In 2015, a joint study by Google and Nielsen found that TV ads can boost branded search queries by up to 20%, especially within the first few hours after an ad airs.
• In 2022, Thinkbox discovered that TV advertising in the UK generates the strongest multiplier effect on search, social, and web traffic of any medium.
• And in 2024, Comscore research found that when TV and digital are coordinated, cross-channel campaigns deliver stronger engagement, with TV ads prompting “second-screen” behavior – audiences searching, scanning QR codes, or engaging on social media in real time.

Put simply: when a campaign captures attention on TV, search demand spikes – often within minutes.

For SEO and PPC professionals, this presents a clear opportunity to anticipate and capitalize on those moments.

How brands have integrated TV and search

Several major brands have already proven that when TV storytelling and search strategy work together, both channels perform better.

Apple: Creating curiosity that fuels search

Apple’s product launches are masterclasses in cross-channel momentum. 

Every time a new iPhone ad airs, search volume for terms like “iPhone 17 Pro Max” or “iPhone 17 release date” skyrockets.

Apple’s branded search traffic increases by up to 40% in the days following a major campaign, according to Semrush.

Apple intentionally designs its TV creative to generate questions – not answer them – encouraging viewers to seek out more details online. 

That’s where Apple’s search-optimized landing pages, YouTube product videos, and paid search campaigns complete the journey.

Progressive: Connecting humor to searchable characters

Progressive’s long-running “Flo” campaign shows how consistent creative storytelling translates into search intent. 

The insurance brand’s TV spots spark curiosity around characters, slogans, and offers – leading to measurable spikes in branded searches such as “Progressive car insurance” and “Flo from Progressive.”

The brand’s media team aligns paid search and display campaigns with national TV flighting schedules, ensuring that when interest peaks, search ads and organic results are ready to capture demand.

Coca-Cola: The shareable, searchable ad

Coca-Cola’s “Share a Coke” campaign is another classic case of TV leading to search. 

The original “Share a Coke” campaign was launched in Australia in 2011 and involved replacing the Coca-Cola logo on bottles with hundreds of popular first names. 

This personalization strategy was a global success, encouraging consumers to find bottles with their names and share them with friends and loved ones, which boosted sales and created emotional connections with the brand.

The latest “Share a Coke” campaign is a global relaunch targeting Gen Z with a focus on digital experiences and authentic, in-person connections. 

It features personalized cans, a digital “Memory Maker” tool for creating shareable videos, and a partnership with McDonald’s. 

Consumers can find names on bottles or use a QR code to customize bottles – a creative hook that’s sent millions to Google searching “custom Coke” or “share a Coke names.”

The campaign’s success wasn’t just creative; it was data-driven. 

By tracking spikes in branded search and social mentions, Coca-Cola refined its targeting and extended the campaign’s life cycle online.

Dig deeper: Hyper-personalization in PPC: Using data to deliver tailored ad experiences

Measuring creative effectiveness with real audience signals

What makes the new “Breaking TV Ads” report particularly valuable is its data-driven framework for measuring creative effectiveness.

Kinetiq’s proprietary ad detection technology identifies every ad that first airs across 210 U.S. DMAs and 15 streaming apps, capturing over a million daily detections. 

DAIVID’s AI then evaluates each ad’s emotional response, attention, and brand recall, creating a creative effectiveness score (CES) – a composite metric that mirrors how audiences actually experience content.

In a media landscape increasingly defined by short attention spans and fragmented screens, this data provides a rare window into why certain stories break through – and how that resonance correlates with downstream behaviors like search and site visits.

As Kinetiq CEO Kevin Kohn put it, the partnership “gives marketers a holistic view of the TV and CTV advertising landscape – not just what aired, but why it resonated.”

That’s exactly the kind of insight performance marketers need to connect the dots between creative resonance and measurable outcomes.

Dig deeper: Your ads are dying: How to spot and stop creative fatigue before it tanks performance

What this means for SEO and PPC strategy

In February 2025, Neal Mohan, the CEO of YouTube, revealed that: 

• “TV has surpassed mobile and is now the primary device for YouTube viewing in the U.S. (by watch time), and according to Nielsen, YouTube has been #1 in streaming watch time in the U.S. for two years.”

So, search marketers can apply the latest findings from the Breaking TV Ads Report in several ways:

• Anticipate search spikes: When a high-emotion or celebrity-driven TV ad launches, expect branded searches to rise. Align PPC budgets, ad copy, and keyword targeting around campaign themes and taglines.
• Optimize for intent moments: TV ads often generate “navigational” queries (brand name) and “informational” ones (product details, offers, or reviews). Ensure that organic content – landing pages, FAQs, and YouTube videos – are optimized to match these queries.
• Sync search campaigns with TV flighting: Use ad scheduling to mirror TV airtime or streaming rollouts. Research from Nielsen Catalina Solutions shows that coordinated campaigns can deliver up to 60% higher conversion lift compared to siloed efforts.
• Track branded search as a creative KPI: Branded search volume is one of the most reliable proxies for ad impact. Use tools like Google Trends or Search Console to monitor shifts after major media bursts.
• Leverage emotional triggers in copy: DAIVID’s data shows that ads evoking strong positive emotions drive higher attention and brand recall. Translate those emotional cues into ad extensions, headlines, and meta descriptions that mirror what audiences feel after seeing the TV spot.

Why the future of performance marketing is cross-channel

Search has long been viewed as a response channel – the final step in a consumer journey. But that view is outdated.

Today’s most successful campaigns use search as a connective tissue between offline inspiration and online action. 

Whether it’s a QR code at the end of a TV ad, a YouTube masthead following a primetime spot, or a Google Shopping ad that captures post-broadcast demand – search is the bridge between storytelling and sales.

As more brands invest in connected TV (CTV) and streaming, the line between “brand” and “performance” marketing will continue to blur. 

Creative effectiveness data helps close that gap – showing which emotional and visual cues are most likely to drive measurable search and conversion behavior.

Ultimately, reports like “Breaking TV Ads” remind us that the most powerful search strategy begins long before the query. 

It begins with attention and emotion, and, increasingly, on the biggest screen in the house.

Dig deeper: How connected TV advertising drives search demand

💾

Search Engine Land turns 19 today.

Nineteen years. Almost two decades of analyzing, explaining, questioning, challenging, obsessing over, and occasionally shaking our heads at whatever Google and the search industry throw our way.

And this past year? The pace of change has made it one of the most transformative since we launched in 2006.

Through all of it, our mission is the same as Day 1: help you make sense of search with clear news, smart analysis, and practical guidance.

Before we look ahead, I want to say thank you — and take a moment to reflect on the past year at Search Engine Land.

Thank you for reading

Seriously, thank you.

Every day, we start with you: what you need to know, what actually matters, and what changes could shape your work today or your strategy six months from now.

We aim to:

• Focus on the stories that matter – not noise or filler.
• Deliver news quickly and clearly.
• Add essential context, expertise, and nuance.
• Be a reliable resource in an industry that seems to shift by the hour.
• Help you see where search is headed — even when the path isn’t obvious.

If you haven’t yet, subscribe to our daily newsletter for a curated wrap-up of everything happening in search. It’s still the easiest way to stay informed without feeling overwhelmed.

Thank you to the Search Engine Land team

Search Engine Land has always punched above its weight for one reason: the people.

A small team can do big, meaningful work when everyone is aligned, mission-driven, and a little obsessed with search.

A huge thank-you to:

• Barry Schwartz. Barry has been covering search for 22 years and still writes with the speed, curiosity, and energy of someone newly in love with the beat. Search would be far less understandable without him.
• Anu Adegbola. Anu has become essential for helping readers navigate nonstop shifts in paid media, analytics, and platform changes. Her clarity and steadiness shine in every piece.
• Angel Niñofranco. Angel keeps our Subject Matter Expert program running. Editing, wrangling, scheduling, coaching, coordinating — if you’ve enjoyed our SME articles, you’ve seen Angel’s impact.
• Kathy Bushman. Kathy makes SMX happen. Her behind-the-scenes work is why our events run smoothly, deliver value, and earn rave reviews year after year.

And to the entire Third Door Media team within Semrush — thank you. Whether or not your name appears here, your work matters and is appreciated.

Top highlights from the past year

In a year defined by uncertainty, it was encouraging to see so many people continue to rely on Search Engine Land as a trusted community resource. And Search Engine Land had a strong 2025.

SMX Advanced returned in person for the first time in 6 years

This was the standout moment of the year. Bringing SMX Advanced back in person after six years felt overdue and incredibly energizing.

Attendance exceeded expectations, sessions were packed, and hallway conversations felt like a reunion of the search marketing community. You could feel how much people missed connecting face-to-face — debating AI’s impact on search, swapping tactics, comparing notes on Google’s latest changes, and simply enjoying each other’s company.

It reaffirmed what we’ve always believed: great things happen when smart marketers share a room. We’re already looking forward to doing it again in Boston, June 3-5.

Defining industry coverage of AI Overviews and the new era of search

This past year brought one of the most dramatic shifts in search since Search Engine Land launched in 2006. Whatever we end up calling this emerging practice, we focused on giving the industry the clarity, context, and reporting it needed.

Readers have told us again and again that Search Engine Land is their go-to source for cutting through the noise during a confusing and often chaotic time. We’re proud that our reporting, explainers, and expert analysis are helping shape the industry’s understanding of where search is headed next.

Subject Matter Expert (SME) program growth

This year brought a surge of new readers and renewed engagement from long-time practitioners. With so many shifts reshaping SEO and PPC – from AI to SERP experiments to advertiser updates – and the continued emergence of GEO, marketers turned to Search Engine Land in record numbers to stay informed.

Our contributors played a significant role in our growth. A huge thank you to all of our excellent SMEs for all the great content and insights you shared in 2025.

Looking ahead: What’s next for Search Engine Land

As we enter our 19th year, our commitment remains unchanged: provide the most trusted, useful coverage of search anywhere.

This year you can expect:

• A fresh new website design.
• Continued breaking news coverage across SEO, PPC, AI search, SERP features, and platform changes.
• Even stronger analysis, guides, and explainers about how search is evolving.
• SMX programming designed around the realities of AI search.
• More expert perspectives, data, and clarity in a year that promises even more disruption.

Save the dates:

• SMX Advanced: June 3-5
• SMX Next: Nov. 18-19

There’s much more to come – and as always, our goal is to give you the insight and intelligence you need to do your best work.

A brief look back to where it all began

On Dec. 11, 2006, Search Engine Land officially launched with a simple idea: search was becoming not just a tool, but a place. A world. A community. A discipline shaping how people find information and how businesses connect with customers.

Nineteen years later, that world has grown in ways none of us could have imagined. But the core idea still holds:

Search Engine Land is a place to stay informed, to learn, to connect, and to understand the engines driving the modern web.

Thank you for 19 incredible years

On behalf of everyone at Search Engine Land and Semrush, thank you for reading, for sharing our stories, for asking hard questions, for supporting our mission, and for caring so deeply about all things search.

Here’s to the rest of 2025 – and to a successful, healthy, and insightful 2026.

Google released the December 2025 core update today, the company announced.

This is the third core update of 2025 and the fourth major Google algorithm update overall. Earlier this year, Google rolled out the August 2025 spam update, which followed the June 2025 core update and the March 2025 core update.

What Google is saying. Google updated its Search Status Dashboard to state:

• “Released the December 2025 core update. The rollout may take up to 3 weeks to complete.”

Google added on LinkedIn:

• “This is a regular update designed to better surface relevant, satisfying content for searchers from all types of sites.”

About core updates. Core updates roll out several times each year. They introduce broad, significant changes to Google’s search algorithms and systems, which is why Google announces them.

• Google also releases some smaller, unannounced core updates.
• It has been a long time since the last core update. While many expected Google to roll out core updates more frequently, that didn’t happen.

Video on this core update. I made this short video a few hours after publishing this story:

What to do if you are hit. Google did not share any new guidance specific to the December 2025 core update. However, in the past, Google has offered advice on what to consider if a core update negatively impacts your site:

• There aren’t specific actions to take to recover. A negative rankings impact may not signal anything is wrong with your pages.
• Google offered a list of questions to consider if your site is hit by a core update.
• Google said you can see some recovery between core updates, but the biggest change would be after another core update.

In short: write helpful content for people and not to rank in search engines.

• “There’s nothing new or special that creators need to do for this update as long as they’ve been making satisfying content meant for people. For those that might not be ranking as well, we strongly encourage reading our creating helpful, reliable, people-first content help page,” Google said previously.

For more details on Google core updates, you can read Google’s documentation.

Previous core updates. Here’s a timeline and our coverage of recent core updates:

• The June 2025 core update was on June 30 and ended on July 17.
• The March 2025 core update was on Mar. 13 and ended on Mar. 27.
• The December 2024 core update was on Dec. 12 and ended on Dec. 18.
• The November 2024 core update was on Nov. 11 and ended on Dec. 5.
• The August 2024 core update was on Aug. 15 and ended on Sept. 3.
• The March 2024 core update was on March 5 and ended on April 19.

Why we care. With any core update, we often see significant volatility in Google search results and rankings. These updates may improve visibility for your site or your clients’ sites, but some may experience fluctuations or even declines in rankings and organic traffic. We hope this update rewards your efforts and drives strong traffic and conversions.

💾